题目内容
14.定义[P,q]为一次函数y=Px+q的特征数.(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且三角形OAB的面积为4(O为原点),求过A,B两点的一次函数的特征数.
分析 (1)根据题意中特征数的概念,可得k-1与k2-1的关系;进而可得k的值;
(2)根据△OAB的面积为4,可得m的方程,解即可得m的值,进而可得答案.
解答 解:(1)∵特征数为[k-1,k2-1]的一次函数为y=(k-1)x+k2-1,
∴k2-1=0,k-1≠0,
∴k=-1;
(2)∵A(-m,0),B(0,-2m),
∴OA=|-m|,OB=|-2m|,
若S△OBA=4,则$\frac{1}{2}$•|-m|•|-2m|=4,m=±2.
∴A(2,0)或(-2,0),B(0,4,)或(0,-4),
∴一次函数为y=-2x-4或y=-2x+4,
∴过A,B两点的一次函数的特征数[-2,-4],[2,4].
点评 此题要理解题目中的定义以及正比例函数的概念,根据正比例函数中的b=0,即可列方程求解.

练习册系列答案
相关题目
5.王先生手中持有四支股票,每只股票的详细信息如下表所示,(单位:元)
请你计算一下,王先生到底赔了还是赚了,赔或赚了多少元?
| 股票名称 | 每股净赚(元) | 股数 |
| 长城 | +23 | 500 |
| 北斗 | -3 | 1000 |
| 白马 | +1.5 | 1000 |
| 海潮 | -7 | 500 |
 如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).
如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).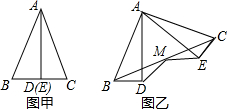 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME. 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.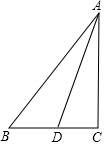 如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.
如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.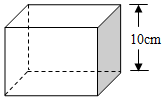 如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?
如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少? 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.