题目内容
3. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.
分析 由题中条件可得Rt△ACD≌Rt△AED,进而得出AC=AE,AC=AE,把△BDE的边长通过等量转化即可得出结论.
解答 解:求△DBE的周长,即求DE+EB+BD的值.
∵AD平分∠CAB,且∠C=90°,DE⊥AB,
∴DC=DE.
可证△ACD≌△AED.∴AC=AE.
又∵AC=BC,
∴DE+EB+BD=DC+EB+BD=BC+EB=AC+EB=AE+EB=AB.
又∵AB=15cm,
∴△DBE的周长=DB+BE+DE=15cm.
∴△DBE的周长是15cm.
故答案为:15c
点评 本题主要考查了角平分线的性质以及全等三角形的判定及性质,能够掌握并熟练运用.

练习册系列答案
相关题目
7.用火柴棒按如图中的方式搭图形,则搭第7个图形所需火柴棒的根数为( )


| A. | 28 | B. | 29 | C. | 34 | D. | 35 |
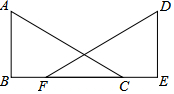 已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.
已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.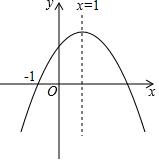 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.