题目内容
6.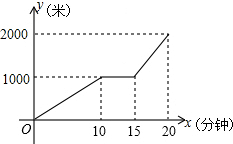 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )| A. | 家到学校的距离是2000米 | |
| B. | 修车耽误的时间是5分钟 | |
| C. | 修车后自行车的速度是每分钟200米 | |
| D. | 修车前比修车后速度快 |
分析 根据图象信息以及速度=$\frac{路程}{时间}$的关系即可解决问题.
解答 解:由图象可知家到学校的距离是2000米,修车耽误的时间是15-10=5分钟,
修车前的速度=$\frac{1000}{10}$=100米/分钟,修车后的速度=$\frac{1000}{5}$=200米/分钟,
故A、B、C正确.
故选D.
点评 本题考查一次函数的应用,知道速度=$\frac{路程}{时间}$,解题的关键是读懂图象信息,是数形结合的好题目,属于中考常考题型.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
14.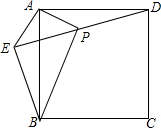 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②③④ | D. | ①②④ |
16.用因式分解法解一元二次方程x(x-3)=x-3时,原方程可化为( )
| A. | (x-1)(x-3)=0 | B. | (x+1)(x-3)=0 | C. | x (x-3)=0 | D. | (x-2)(x-3)=0 |
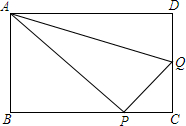 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动.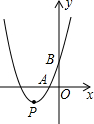 如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$.
如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$. 如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.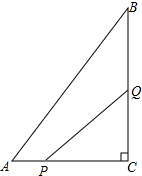 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?