题目内容
19.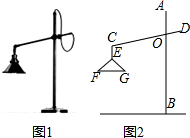 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
分析 (1)由EF=EG可知∠G=∠F=40°,由三角形的内角和为180°可求出∠FEG的大小,根据已知条件可得知∠CEF=∠CEG,由∠CEF+∠FEG+∠GEC为周角可得出结论;
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,找出四边形CHNM为长方形,在Rt△CMO中由三角函数值求出CM的长度,再结合点G到OB的距离为12cm可求出HG的长度,由△EFG为等腰三角形可得知FG=2HG,从而得出结论.
解答 解:(1)∵EF=EG,∠F=40°,
∴∠G=40°,∠FEG=180°-∠F-∠G=100°,
∵灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,
∴∠CEG=∠CEF=$\frac{360°-∠FEG}{2}$=130°.
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,如图所示.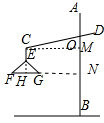
∵CE∥AB,FG处于水平位置,EM⊥AB,
∴四边形CHNM为长方形,CH⊥FG,
∴CM=HN.
在Rt△OMC中,OC=20cm,∠COM=70°,∠OMC=90°,
∴CM=OC•sin∠COM≈20×0.940=18.8(cm),
∵GN=12cm,HN=CM,
∴HG=CM-GN=6.8(cm).
∵EF=EG,CH⊥FG,
∴FH=HG=$\frac{1}{2}$FG,
∴FG=2×6.8=13.6(cm).
答:灯罩的宽度为13.6cm.
点评 本题考查了长方形的判定及性质、解直角三角形以及等腰三角形的性质,解题的关键:(1)求出∠FEG的度数;(2)在直角△CMO中求出CM的长度.本题属于中档题,(1)难度不大;(2)稍显复杂,解决该题型题目时,需要借助直角三角形及角的三角函数值来求值.

练习册系列答案
相关题目
14.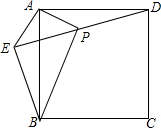 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②③④ | D. | ①②④ |
4.下列四个图形中是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.若427+41000+4n为完全平方数,则正整数n满足( )
| A. | n≥1972 | B. | n≤1972 | C. | n≥1973 | D. | n≤1970 |
 如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.
如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.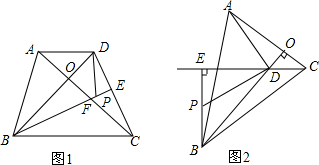
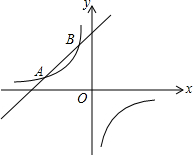 如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4). 如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.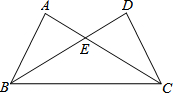 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.