题目内容
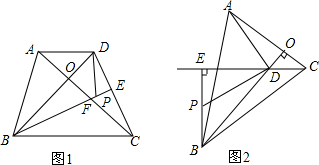
2.已知:如图.BD=BC=2AC,∠DBC=∠ACB,CD交线段AB于点E.(1)如图①,当∠ACB=90°时.則线段DE、CE之间的数量关系为DE=2CE;
(2)如图②,当∠ACB=120°时.试探究DE与CE之间的数量关系,并说明现由;
(3)如明③,在(2)的条件下,点F是边BC的中点,连接DF,DF与AB交于点G,试探究DG与FG之间的数量关系.
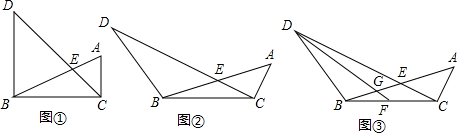
分析 (1)易证△DEB∽△CEA,然后只需运用相似三角形的性质就可解决问题;
(2)过点B作BH⊥DC于H,如图2.根据等腰三角形的性质可得∠D=∠BCD=30°,DH=CH,从而可得BH=AC,∠BHE=∠ACE,进而可得△BHE≌△ACE,则有HE=CE,即可证到DE=3EC;
(3)延长DF到点N,使得FN=DF,连接NB、NC,如图3,易证四边形DCNB是平行四边形,从而可得DC∥BN,DC=BN,即可得到△DGE∽△NGB,然后由相似三角形的对应边成比例,求得DG与NG的比值,继而求得答案.
解答 解:(1)∵∠ACB=90°,∠DBC=∠ACB,
∴∠DBC=90°,
∴∠DBC+∠ACB=180°,
∴DB∥AC,
∴△DEB∽△CEA,
∴$\frac{DE}{EC}$=$\frac{DB}{CA}$.
∵BD=BC=2AC,
∴DE=2CE;
故答案为:DE=2CE;
(2)猜想:DE=3CE.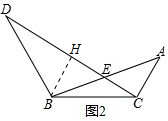
理由:过点B作BH⊥DC于H,如图2.
又∵BD=BC,∠DBC=∠ACB=120°,
∴∠D=∠BCD=30°,DH=CH,
∴DB=2BH,∠ACE=90°,
∴BH=AC,∠BHE=∠ACE.
在△BHE和△ACE中,
$\left\{\begin{array}{l}{∠BHE=∠ACE}\\{∠BEH=∠AEC}\\{BH=AC}\end{array}\right.$,
∴△BHE≌△ACE,
∴HE=CE,
∴DH=HC=2EC,
∴DE=DH+HE=2EC+EC=3EC;
(3)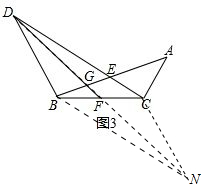 延长DF到点N,使得FN=DF,连接NB、NC,如图3,
延长DF到点N,使得FN=DF,连接NB、NC,如图3,
∵BF=CF,FN=DF,
∴四边形DCNB是平行四边形,
∴DC∥BN,DC=BN,
∴△DGE∽△NGB,$\frac{DE}{BN}$=$\frac{3EC}{4EC}$=$\frac{3}{4}$,
∴$\frac{DG}{NG}$=$\frac{DE}{NB}$=$\frac{3}{4}$.
设DG=3k,则有NG=4k,DN=7k,
∴DF=$\frac{1}{2}$DN=$\frac{7k}{2}$,
∴GF=DF-DG=$\frac{7k}{2}$-3k=$\frac{1}{2}$k,
∴DG=6GF.
点评 此题属于相似三角形的综合题,主要考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、等腰三角形的性质以及平行线的判定与性质.注意准确作出辅助线是解此题的关键.

| A. | a3•a3=a9 | B. | (a3)2=a5 | C. | (2ab2)3=6a3b6 | D. | (-a)7÷(-a)2=-a5 |
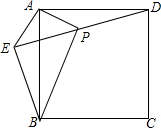 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②③④ | D. | ①②④ |
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
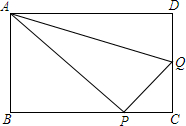 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动.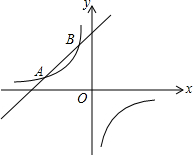 如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4). 如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.