题目内容
15.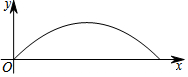 某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系(1)求出抛物线的函数解析式
(2)当m=10时,试判断足球能否射入球门,并说明理由
(3)球员射门时,若满足t2>m>t1,球部越过球门,求t1的最小值及t2的最大值.
分析 (1)设抛物线的解析式为y=a(x-6)2+3,将(0,0)代入可得;
(2)求出x=10时y的值,判断即可;
(3)分别求出y=0和y=12时x的值即可知其范围.
解答 解:(1)设抛物线的解析式为y=a(x-6)2+3,
将点(0,0)代入,得:36a+3=0,
解得:a=-$\frac{1}{12}$,
∴抛物线解析式为y=-$\frac{1}{12}$(x-6)2+3;
(2)当m=10即x=10时,y=-$\frac{1}{12}$(10-6)2+3=$\frac{5}{3}$,
∵0<$\frac{5}{3}$<2.4,
∴足球能射入球门;
(3)当y=0时,-$\frac{1}{12}$(x-6)2+3=0,
解得:x=0或x=12;
当y=2.4时,-$\frac{1}{12}$(x-6)2+3=2.4,
解得:x=6+$\frac{6\sqrt{5}}{5}$或x=6-$\frac{6\sqrt{5}}{5}$,
∴6+$\frac{6\sqrt{5}}{5}$≤x≤12,
即t1的最小值为6+$\frac{6\sqrt{5}}{5}$,t2的最大值为12.
点评 本题主要考查二次函数的应用,根据题意弄清球不过球门时对应的函数值的状态是关键.

练习册系列答案
相关题目
5.下列各式的值一定是正数的是( )
| A. | |a| | B. | $\sqrt{a^2}$ | C. | $\frac{1}{a^2}$ | D. | $\root{3}{a}$ |
10.矩形ABCD的边AB=3 cm,AD=4 cm,以A为圆心,4 cm为半径作⊙A,则点C与⊙A的位置关系为( )
| A. | 点C在⊙A内 | B. | 点C不一定在⊙A外 | C. | 点C在⊙A上 | D. | 点C在⊙A外 |
4.若一次函数y=kx+2经过点(-1,1),则下面说法正确的是( )
| A. | y随x的增大而增大 | B. | 图象经过点(3,-1) | ||
| C. | 图象不经过第二象限 | D. | 图象与函数y=-x图象有一个交点 |
 如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.
如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.

 如图AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F为AD的中点,连结EF.
如图AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F为AD的中点,连结EF.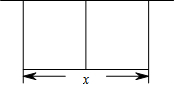 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)