题目内容
19.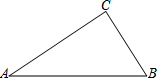 如图,己知△ABC
如图,己知△ABC(1)用直尺和圆规作出⊙O,使⊙O经过A,C两点,且圆心O在AB边上(不写作法,保留作图痕迹)
(2)在(1)中,若∠CAB=30°,∠B=60°且⊙O的半径为1,试求出AB的长.
分析 (1)根据弦的垂直平分线经过圆心,可以先作出AC的垂直平分线,交AB于点O,再以O为圆心,AO长为半径画圆即可;
(2)先连接CO,根据∠CAB=30°,∠B=60°,求得∠BCO=∠B=60°,进而得到BO=CO=1,即可得出AB=2.
解答 解:(1)如图所示,⊙O即为所求;
(2)如图所示,连接CO,
∵∠CAB=30°,∠B=60°,
∴∠ACB=90°,
又∵AO=CO=1,
∴∠A=∠ACO=30°,
∴∠BCO=90°-30°=60°,
∴∠BCO=∠B=60°,
∴BO=CO=1,
∴AB=2.
点评 本题主要考查了复杂作图以及垂径定理的运用,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.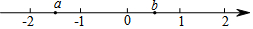 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )
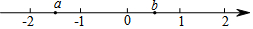 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b>0 | B. | a-b>0 | C. | $\frac{a}{b}$>0 | D. | b2<a2 |
10.矩形ABCD的边AB=3 cm,AD=4 cm,以A为圆心,4 cm为半径作⊙A,则点C与⊙A的位置关系为( )
| A. | 点C在⊙A内 | B. | 点C不一定在⊙A外 | C. | 点C在⊙A上 | D. | 点C在⊙A外 |
14.若单项式x2ym-n与单项式-$\frac{1}{2}{x^{2m+n}}{y^3}$是同类项,那么这两个多项式的和是( )
| A. | $\frac{1}{2}{x^4}{y^6}$ | B. | $\frac{1}{2}{x^2}{y^3}$ | C. | $\frac{3}{2}{x^2}{y^3}$ | D. | $-\frac{1}{2}{x^2}{y^3}$ |
4.若一次函数y=kx+2经过点(-1,1),则下面说法正确的是( )
| A. | y随x的增大而增大 | B. | 图象经过点(3,-1) | ||
| C. | 图象不经过第二象限 | D. | 图象与函数y=-x图象有一个交点 |
8.以下关于$\sqrt{8}$的叙述,错误的是( )
| A. | 面积为8的正方形边长是$\sqrt{8}$ | B. | $\sqrt{8}$是无理数 | ||
| C. | 在数轴上没有对应$\sqrt{8}$的点 | D. | $\sqrt{8}$介于整数2和3之间 |
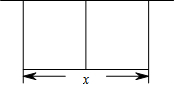 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2) 如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF
如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF