题目内容
16.如图,在矩形ABCD中.AB=3厘米,BC=7厘米.动点E从点D出发向点A运动,速度为每秒1厘米,同时动点F从点B出发向点C运动,速度为每秒2厘米.当点F到达点C时,两点同时停止运动,设运动时间为t秒,连结EF,将矩形沿EF对折.(1)当t=1时,求EF的长;
(2)当t为何值时,矩形ABCD左边无重叠部分(阴影部分)为矩形?

分析 (1)作EH⊥BC于H,根据矩形的判断和性质得到EH=CD=3,根据题意求出FH,根据勾股定理计算即可;
(2)根据矩形的性质得到∠NFC=90°,NF=AB=3,根据翻转变换的性质得到NF=NE,根据题意列式计算即可.
解答 解:(1)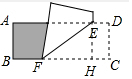 作EH⊥BC于H,
作EH⊥BC于H,
则四边形DEHC是矩形,
∴EH=CD=3,
当t=1时,HC=DE=1,BF=2,
则FH=7-2-1=4,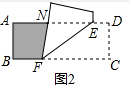
由勾股定理得,EF=$\sqrt{F{H}^{2}+E{H}^{2}}$=5;
(2)如图2,当ABFN是矩形时,∠NFC=90°,NF=AB=3,
由折叠的性质可知,∠NFE=∠CFE=45°,
∴NF=NE,即7-t-2t=3,
解得,t=$\frac{4}{3}$,
则当t=$\frac{4}{3}$时,矩形ABCD左边无重叠部分为矩形.
点评 本题考查的是翻转变换的性质、矩形的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
4.若一次函数y=kx+2经过点(-1,1),则下面说法正确的是( )
| A. | y随x的增大而增大 | B. | 图象经过点(3,-1) | ||
| C. | 图象不经过第二象限 | D. | 图象与函数y=-x图象有一个交点 |
1.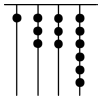 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )| A. | 517 | B. | 84 | C. | 336 | D. | 1326 |
8.以下关于$\sqrt{8}$的叙述,错误的是( )
| A. | 面积为8的正方形边长是$\sqrt{8}$ | B. | $\sqrt{8}$是无理数 | ||
| C. | 在数轴上没有对应$\sqrt{8}$的点 | D. | $\sqrt{8}$介于整数2和3之间 |
 如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.
如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.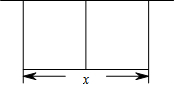 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)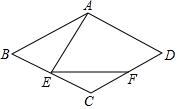 如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF.
如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF.