题目内容
17. 如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.
如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.(1)请写出图中任意两对相等线段:AC=AD,BC=BD;
(2)证明:BE=BF.
分析 (1)根据线段垂直平分线的性质解答;
(2)证明△ACB≌△ADB,根据全等三角形的性质证明结论.
解答 解:(1)∵AB是CD的垂直平分线,
∴AC=AD,BC=BD,
故答案为:AC=AD;BC=BD;
(2)∵AC=AD,E,F是AC,AD的中点,
∴AE=AF,
∵AC=AD,AB⊥CD,
∴∠CAB=∠DAB,
在△ACB和△ADB中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAB=∠DAB}\\{AB=AB}\end{array}\right.$,
∴△ACB≌△ADB,
∴BE=BF.
点评 本题考查的是线段垂直平分线的性质、全等三角形的判定和性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
5.下列各式的值一定是正数的是( )
| A. | |a| | B. | $\sqrt{a^2}$ | C. | $\frac{1}{a^2}$ | D. | $\root{3}{a}$ |
9.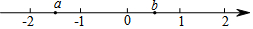 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )
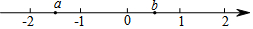 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b>0 | B. | a-b>0 | C. | $\frac{a}{b}$>0 | D. | b2<a2 |
 如图,在平行四边形ABCD中,EF∥AB交AD于E交BD于F,DE:EA=3:4,EF=6,则CD的长为14.
如图,在平行四边形ABCD中,EF∥AB交AD于E交BD于F,DE:EA=3:4,EF=6,则CD的长为14. 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$). 如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E.
如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E. 如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.
如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.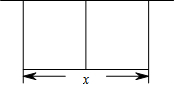 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)