题目内容
19.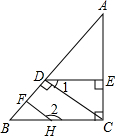 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).解:垂直.理由如下:
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°(①在同一平面内,垂直于同一直线的两条直线互相平行).
∴DE∥BC(②同位角相等,两直线平行)
∴∠1=∠DCB(③两直线平行,内错角相等)
∵∠1与∠2互补(已知).
∴∠DCB与∠2互补
∴DC∥FH(④同旁内角互补,两直线平行)
∴∠BFH=∠CDB(⑤两直线平行,同位角相等)
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFH=90°(⑥等量代换).
∴HF⊥AB.
分析 根据AC⊥BC,DE⊥AC,易证DE∥BC,于是∠1=∠DCB,而∠1与∠2互补,那么∠2+∠DCB=180°,从而可证FH∥CD,结合CD⊥AB,易得∠HFD=90°,即HF⊥AB.
解答 解:垂直.理由如下:
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°(在同一平面内,垂直于同一直线的两条直线互相平行)
∴DE∥BC(同位角相等,两直线平行),
∴∠1=∠DCB(两直线平行,内错角相等);
∵∠1与∠2互补(已知),
∴∠DCB与∠2互补,
∴DC∥FH(同旁内角互补,两直线平行),
∴∠BFH=∠CDB(两直线平行,同位角相等);
∵CD⊥AB,
∴∠CDB=90°,
∴∠HFB=90°(等量代换),
∴HF⊥AB.
故答案是:①在同一平面内,垂直于同一直线的两条直线互相平行;②同位角相等,两直线平行;③两直线平行,内错角相等;④同旁内角互补,两直线平行;⑤两直线平行,同位角相等;⑥等量代换.
点评 本题考查了平行线的判定与性质.熟练掌握平行线的性质及判定是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.下面各条件中,能判定四边形是平行四边形的是( )
| A. | 对角线互相垂直 | B. | 两组对边分别相等 | ||
| C. | 一组对角相等 | D. | 一组对边相等,另一组对边平行 |
7.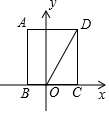 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )| A. | (-$\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,1)或(1,-$\sqrt{3}$) |
14. 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
8.已知:x、y满足|x+2y+3|+(2x+y)2=0,则x-y=( )
| A. | 7 | B. | 5 | C. | 3 | D. | 1 |
 如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;
如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;