题目内容
9. 如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;
如图 A(0,-4)、B(-2,0),M为直线l1:x=-1上一点,N为直线l2:y=x+3上一点.若以A、B、M、N为顶点的四边形是平行四边形,求所有满足条件的点N的坐标;点拨:平行四边形转化为点的平移或平移的全等三角形;
认真审题,数形结合(画尽量准确的图),分类讨论(AB为边或对角线)
分析 当AB为边时,根据点A、B和点M的横坐标,利用平行四边形的性质即可得出点N的横坐标,再利用一次函数图象上点的坐标特征即可得出点N的坐标;当AB为对角线时,设AB的中点为C,根据点A、B的坐标可得出点C的坐标,由点C的坐标结合点M的横坐标即可得出点N的横坐标,再利用一次函数图象上点的坐标特征即可得出点N的坐标.综上即可得出结论.
解答 解:当AB为边时,∵A(0,-4)、B(-2,0),点M在直线x=-1上,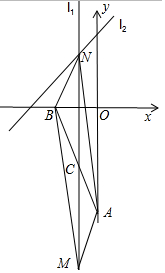
∴点N的横坐标为-2-1=-3.
当x=-3时,y=x+3=0,
∴此时点N的坐标为(-3,0);
当AB为对角线时,设AB的中点为C,如图所示.
∵A(0,-4)、B(-2,0),
∴点C的坐标为(-1,-2).
∵四边形ANBM为平行四边形,
∴点M、N的横坐标为-1.
当x=-1时,y=x+3=2,
∴此时点N的坐标为(-1,2).
综上所述:所有满足条件的点N的坐标为(-3,0)和(-1,2).
点评 本题考查了一次函数图象上点的坐标特征以及平行四边形的性质,根据平行四边形的性质找出点N的横坐标是解题的关键.

练习册系列答案
相关题目
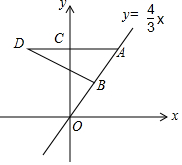 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.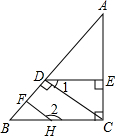 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).