题目内容
4.解三元一次方程组$\left\{\begin{array}{l}{a-b+c=0}\\{4a+2b+c=3}\\{25a+5b+c=60}\end{array}\right.$.分析 根据解三元一次方程组的方法可以解答本题.
解答 解:$\left\{\begin{array}{l}{a-b+c=0}&{①}\\{4a+2b+c=3}&{②}\\{25a+5b+c=60}&{③}\end{array}\right.$,
②-①,得
3a+3b=3,④
③-②,得
21a+3b=57,⑤
⑤-④,得
18a=54,
解得,a=3,
将a=3代入④,得
b=-2,
将a=3,b=-2代入①,得
c=-5,
故原方程组的解是$\left\{\begin{array}{l}{a=3}\\{b=-2}\\{c=-5}\end{array}\right.$.
点评 本题考查解三元一次方程组,解答本题的关键是明确解三元一次方程组的方法,利用消元的思想解答.

练习册系列答案
相关题目
12.一元二次方程式x2-8x=48可表示成(x-a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )
| A. | 20 | B. | 12 | C. | -12 | D. | -20 |
9.若3am+2b与ab2n-1是同类项,则m+n的值是( )
| A. | -1 | B. | -5 | C. | 2 | D. | 0 |
16.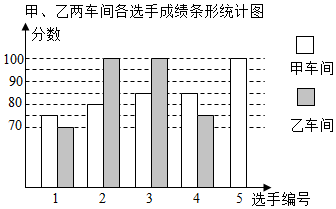 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
根据图标信息,解答问题:
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲车间 | 75 | 80 | 85 | 85 | 100 |
| 乙车间 | 70 | 100 | x | 75 | 80 |
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
13.外心在三角形的一边上的三角形形状一定为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
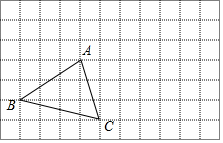 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.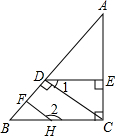 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).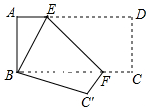 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落到点C′处,折痕为EF.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落到点C′处,折痕为EF.