题目内容
7.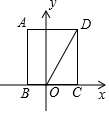 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )| A. | (-$\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,1)或(1,-$\sqrt{3}$) |
分析 根据矩形的性质得到CD=AB=2$\sqrt{3}$,∠DCO=90°,根据已知条件得到∠DOC=60°,OC=2,①当顺时针旋转至△OD′C′时,过C′作C′E⊥OD′于E,②当逆时针旋转至△OD″C″时,如图,过C″作C″E⊥OD″于F,解直角三角形即可得到结论.
解答 解: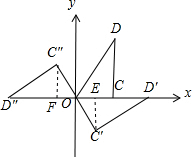 在矩形ABCD中,
在矩形ABCD中,
∵CD=AB=2$\sqrt{3}$,∠DCO=90°,
∵OD=4,
∴∠DOC=60°,OC=2,
①当顺时针旋转至△OD′C′时,如图,∠D′OC′=∠DOC=60°,OC′=OC=2,
过C′作C′E⊥OD′于E,则OE=$\frac{1}{2}$OC′=1,C′E=$\frac{\sqrt{3}}{2}$OC′=$\sqrt{3}$,
∴C′(1,-$\sqrt{3}$),
②当逆时针旋转至△OD″C″时,如图,∠D″OC″=∠DOC=60°,OC″=OC=2,
过C″作C″E⊥OD″于F,则OF=$\frac{1}{2}$OC″=1,C″F=$\frac{\sqrt{3}}{2}$OC′=$\sqrt{3}$,
∴C″(-1,$\sqrt{3}$),
综上所述:点C对应点的坐标是(1,-$\sqrt{3}$),(-1,$\sqrt{3}$),
故选:C.
点评 本题考查了坐标与图形变换-旋转,矩形的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2.已知:①平行四边形 ②矩形 ③菱形 ④等腰三角形 ⑤等腰梯形.这5种图形中,既是中心对称图形,又是轴对称图形的有( )
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
12.一元二次方程式x2-8x=48可表示成(x-a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )
| A. | 20 | B. | 12 | C. | -12 | D. | -20 |
16.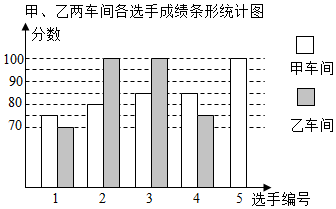 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
根据图标信息,解答问题:
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲车间 | 75 | 80 | 85 | 85 | 100 |
| 乙车间 | 70 | 100 | x | 75 | 80 |
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
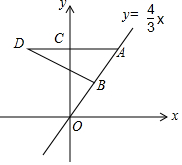 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.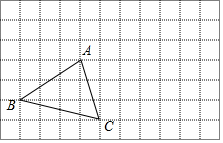 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.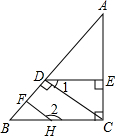 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空).