Question

18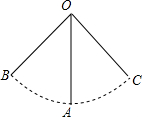．某新建小区里安装了一架秋千，如图是一个小孩荡秋千的侧面示意图，秋千的链子OA的长度为3米，秋千向两边摆动的最大角度相同，且最大角度的和∠BOC恰好为90°，则它摆至最高位置与最低位置的高度之差是（　　）

• A． 3$\sqrt{2}$米
• B． $\frac{3\sqrt{2}}{2}$米
• C． $\frac{6-3\sqrt{2}}{2}$米
• D． 无法确定

Answer 1

分析 连接BC交OA于点M，线段AM的长度就是最高位置与最低位置的高度之差，根据等腰直角三角形的性质即可解决．

解答 解：连接BC交OA于点M．
∵OB=OC，∠AOB=∠AOC，
∴OA⊥BC，
∴BM=MC，
∴OM=$\frac{1}{2}$BC，
∵∠BOC=90°，OB=OC=3，
∴BC=3$\sqrt{2}$，
∴OM=$\frac{3\sqrt{2}}{2}$，
∴AM=OA-OM=3-$\frac{3\sqrt{2}}{2}$=$\frac{6-3\sqrt{2}}{2}$．
故选C．

点评 本题考查解直角三角形、垂径定理、等腰直角三角形的性质等知识，理解高度差的意义是解题的关键，学会转化的思想，求AM只要求出OM即可．