题目内容
3.已知关于a的一元二次方程2a2+8a=k有两个相等的实数根,求关于x的分式方程$\frac{x}{x+1}+k+3=\frac{a+5}{1-x}$的解.分析 首先根据一元二次方程有两根求出k的值,进而解分式方程即可.
解答 解:∵关于a的一元二次方程2a2+8a=k有两个相等的实数根,
∴△=64+8k=0,
∴k=-8,
∴a1=a2=-2,
∴关于x的分式方程为$\frac{x}{x+1}$-5=$\frac{3}{1-x}$,
解得x=2,
经检验,x=2是原分式方程的解,
∴原分式方程的解为x=2.
点评 本题主要考查了根的判别式与解分式方程的知识,解答本题的关键是根据根的判别式的意义求出k的值,此题难度不大.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.已知x>y,m≠0,则下列说法中,正确的是( )
| A. | m+x>m+y | B. | m-x>m-y | C. | mx>my | D. | m2x≥m2y |
18.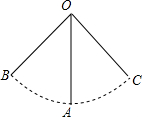 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )| A. | 3$\sqrt{2}$米 | B. | $\frac{3\sqrt{2}}{2}$米 | C. | $\frac{6-3\sqrt{2}}{2}$米 | D. | 无法确定 |
8.程程家进行装修,程程的爸爸想用某种图形的地砖无间隙地铺设地面,下列的多边形地砖不能用于此次地面的铺设的是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
15.下列说法正确的是( )
| A. | “购买一张彩票就中奖”是不可能事件 | |
| B. | “抛掷一枚质地均匀的骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应做普查 | |
| D. | 从扇形统计图中,可以直接得到各部分的具体数值 |
 如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.
如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.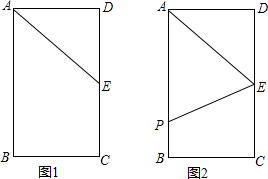
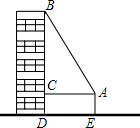 如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?
如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?