题目内容
8. 如图,四边形ABCD中,连接AC,BD,△ABC是等边三角形,∠ADC=30°,并且AD=4.5,BD=7,5,则CD的长为6.
如图,四边形ABCD中,连接AC,BD,△ABC是等边三角形,∠ADC=30°,并且AD=4.5,BD=7,5,则CD的长为6.
分析 首先以CD为边作等边△CDE,连接AE,利用全等三角形的判定得出△BCD≌△ACE,进而求出DE的长即可.
解答 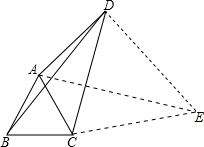 解:如图,以CD为边作等边△CDE,连接AE.
解:如图,以CD为边作等边△CDE,连接AE.
∵∠BCD=∠BCA+∠ACD=∠DCE+∠ACD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴BD=AE.
又∵∠ADC=30°,
∴∠ADE=90°.
在Rt△ADE中,AE=7.5,AD=4.5,
于是DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=6,
∴CD=DE=6.
故答案为6.
点评 此题主要考查了等边三角形的性质以及全等三角形的判定与性质,根据已知得出∠ADE=90°是解题关键.

练习册系列答案
相关题目
3. 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )| A. | n可以为3和4 | |
| B. | n可以为所有正偶数 | |
| C. | n可以为所有大于2的整数 | |
| D. | 正整数中所有3的倍数的数都可以为n值 |
20.已知线段AB=6cm,点C是直线AB上一点,BC=4cm,则线段AC的长度是( )
| A. | 10cm | B. | 2cm | C. | 2cm或10cm | D. | 5cm |
18.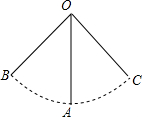 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )| A. | 3$\sqrt{2}$米 | B. | $\frac{3\sqrt{2}}{2}$米 | C. | $\frac{6-3\sqrt{2}}{2}$米 | D. | 无法确定 |
 已知:点P为正方形ABCD内一点,连接PA、PB、PC,若AP2+CP2=2PB2,
已知:点P为正方形ABCD内一点,连接PA、PB、PC,若AP2+CP2=2PB2, 如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.
如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长. 如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.
如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.