题目内容
15. (一)阅读
(一)阅读求x2+6x+11的最小值.
解:x2+6x+11
=x2+6x+9+2
=(x+3)2+2
由于(x+3)2的值必定为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.
(二)解决问题
(1)若m2+2mn+2n2-6n+9=0,求($\frac{m}{n}$)-3的值;
(2)对于多项式x2+y2-2x+2y+5,当x,y取何值时有最小值.
分析 (1)根据完全平方公式把已知条件变形得到(m+n)2+(n-3)2=0,再根据非负数的性质求出m、n,然后把m、n的值代入计算即可;
(2)原式利用完全平方公式变形,再利用非负数的性质求出最小值,以及x与y的值即可.
解答 解:(1)解:原式可变为m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0,
∴m+n=0且n-3=0,
∴m=-3,n=3,
∴($\frac{m}{n}$)-3=${(\frac{-3}{3})}^{-3}$=(-1)-3=-1;
(2)原式=x2+y2-2x+2y+1+1+3
=(x2-2x+1)+(y2+2y+1)+3
=(x-1)2+(y+1)2+3
因为(x-1)2和(y+1)2的值必定为非负数,
所以当x=1,y=-1时,x2+y2-2x+2y+5有最小值.
点评 此题考查了因式分解-运用公式法,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
6.下列命题的逆命题是真命题的有( )
(1)对顶角相等;
(2)全等三角形的面积相等;
(3)线段垂直平分线上的点到这条线段两个端点的距离相等;
(4)如果x>0,那么x2>0.
(1)对顶角相等;
(2)全等三角形的面积相等;
(3)线段垂直平分线上的点到这条线段两个端点的距离相等;
(4)如果x>0,那么x2>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.计算(-a+2b)2-(-a-2b)2的结果是( )
| A. | -8ab | B. | -4ab | C. | 8ab | D. | 4ab |
 已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.

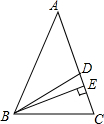 如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.
如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.