题目内容
20.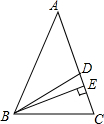 如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.
如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.
分析 根据三角形的内角和等于180°表示出∠ABC,再根据角平分线的定义表示出∠CBD,根据直角三角形两锐角互余表示出∠CBE,然后根据∠DBE=∠CBD-∠CBE整理即可得解.
解答 解:在△ABC中,∠ABC=180°-∠A-∠C,
∵BD平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$(180°-∠A-∠C),
∵BE⊥AC,
∴∠CBE=90°-∠C,
∴∠DBE=∠CBD-∠CBE=$\frac{1}{2}$(180°-∠A-∠C)-(90°-∠C)=$\frac{1}{2}$(∠C-∠A),
∵∠C-∠A=20°,
∴∠DBE=$\frac{1}{2}$×20°=10°.
故答案为:10°.
点评 本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余的性质,熟记定理与性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
8.某电器超市销售每台进价分别为400元、340元的A、B两种型号的豆浆机.下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)第三周该超市采购这两种型号的豆浆机共20台,如果全部售出,要使销售利润不少于1600元,求至少购进A种型号豆浆机多少台?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 3500 |
| 第二周 | 4台 | 10台 | 6000 |
(1)求A、B两种型号的电风扇的销售单价;
(2)第三周该超市采购这两种型号的豆浆机共20台,如果全部售出,要使销售利润不少于1600元,求至少购进A种型号豆浆机多少台?
10. 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=40°,则∠2=( )
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=40°,则∠2=( )
 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=40°,则∠2=( )
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=40°,则∠2=( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3. (一)阅读
(一)阅读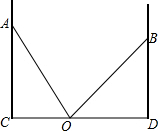 如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米.
如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米. 如图,已知点C为AB上一点,AC=15cm,CB=$\frac{3}{5}$AC,D,E分别为AC,AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=15cm,CB=$\frac{3}{5}$AC,D,E分别为AC,AB的中点,求DE的长.