题目内容
6.在Rt△ABC中,∠ABC=2∠ACB,延长AB至点D,使BD=BC,点E是直线BC上一点,点F是直线AC上一点,连接DE.连接EF,且∠DEF=∠DBC.(1)如图1,若∠D=∠EFC,AB=$\sqrt{3}$,求AC的长.
(2)如图2,当∠BAC=45°,点E为线段BC的延长线上,点F在线段AC的延长线上时,求证:CF=$\sqrt{2}$BE.
(3)如图3,当∠BAC=90°,点E为线段CB的延长线上,点F在线段CA的延长线上时,猜想线段CF与线段BE的数量关系,并证明猜想的结论.
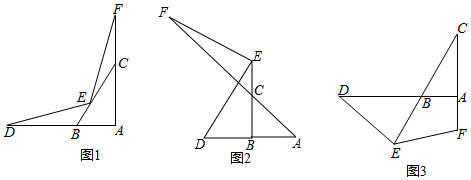
分析 (1)由题意推出∠ACB=30°,由此即可解决问题.
(2)延长DB到N,使得DN=EC.只要证明△NDE≌△CEF,△ENB是等腰直角三角形即可解决问题;
(3)CF=$\sqrt{3}$BE.如图3中,连接CD、DF、作NE⊥CE交AD的延长线于N,在线段CE上截取一点M,使得FM=FE.只要证明△EDN≌△CMF,推出NE=CF,即可解决问题.
解答 (1)解:∵∠BAC=90°,∠ABC=2∠ACB,
∴∠ACB=30°
在Rt△ABC中,∵∠BAC=90°,AB=$\sqrt{3}$,∠ACB=30°,
∴BC=2AB=2$\sqrt{3}$,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3.
(2)证明:延长DB到N,使得DN=EC.
∵∠ABC=2∠ACB,∠BAC=45°,
∴∠ABC=90°,∠A=∠BCA=45°,
∴BC=AB=BD,∵DN=EC,
∴BN=BE,
∴∠N=45°,
∵ECF=∠BCA=45°,
∴∠N=∠ECF,
∵∠NDE=90°+∠DEB,∠FEC=90°+∠DEB,
∴∠NDE=∠FEC,
∴△NDE≌△CEF,
∴EN=CF,
∵EN=$\sqrt{2}$BE,
∴CF=$\sqrt{2}$BE.
(3)结论:CF=$\sqrt{3}$BE.
理由:延长BA至点N,使得BN=BE,连接NE,作BM⊥EN于M.
∵BD=BC,BN=BE,
∴DN=EC,
∵∠ABC=60°,
∴∠BEN=∠N=30°,
∴∠C=∠N,
∵∠DBC=∠DEF,
∴∠D+∠DEB=∠DEB+∠CEF,
∴∠D=∠CEF,
∴△CEF≌△NDE,
∴CF=EN,
∵BE=BN,BM⊥EN,
∴EM=MN,
在Rt△BEM中,EM=EB•cos30°=$\frac{\sqrt{3}}{2}$EB,
∴CF=EN=2EM=$\sqrt{3}$EB.
∴CF=$\sqrt{3}$BE.
点评 本题考查三角形综合题、全等三角形的判定和性质、四点共圆、圆的有关性质、勾股定理、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用四点共圆创造条件解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.
| A. | $\left\{\begin{array}{l}{x+y=500}\\{(1+4%)x+(1+3%)y=500×(1+3.4)}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=500}\\{3%x+4%y=3.4%}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=500}\\{(1+3%)x+(1+4%)y=500×(1+3.4%)}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=500}\\{4%x+3%y=500×3.4%}\end{array}\right.$ |
| A. | a=4,b=5 | B. | a=-4,b=5 | C. | a=4,b=-5 | D. | a=-4,b=-5 |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 2 |
 抛物线y=x2+bx+3与x轴正半轴交于A、B两点,(A点在B点左边),与y轴正半轴交于C点,对称轴为x=2,求抛物线的解析式.
抛物线y=x2+bx+3与x轴正半轴交于A、B两点,(A点在B点左边),与y轴正半轴交于C点,对称轴为x=2,求抛物线的解析式.