题目内容
16.已知点A(0,3),B(5,0),点C,D分别在直线x=2与x=3上,且CD∥x轴,则AC+CD+DB的最小值为3$\sqrt{2}$+1.分析 可以把直线x=2,x=3形成的图形理解为一条河,CD为一座桥,求AC+CD+DB的最小值,可转化为“修桥问题”.
解答 解:作法如图,
过A作直线x=2的垂线,垂足为M,连接BM交直线x=3于D点,过D点作直线x=2的垂线,垂足为C点,
此时,AC+CD+DB的最小,AC+CD+DB=MD+CD+DB=BM+CD=$\sqrt{{3}^{2}+(5-2)^{2}}$+CD=3$\sqrt{2}$+CD=3$\sqrt{2}$+1.
故答案为:3$\sqrt{2}$+1.
点评 本题考查了最短路线问题,解题的关键是将实际问题转化为数学模型“修桥问题”,结合图形进行计算.

练习册系列答案
相关题目
7.下列几幅图是正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
11.-2100×0.5100×(-1)2013-$\frac{1}{2}$计算结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | 0 |
5.下列各数中,最小的数是( )
| A. | -3 | B. | -$\frac{1}{2}$ | C. | 2 | D. | 0 |
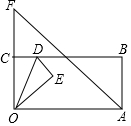 如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.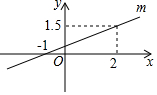 如图所示,直线m是一次函数y=kx+b的图象.
如图所示,直线m是一次函数y=kx+b的图象.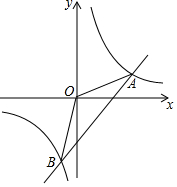 如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0
如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0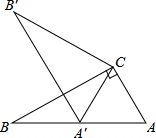 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )