题目内容
16.某花卉基地种植了郁金香和玫瑰两种花卉共30亩,有关数据如表:| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
分析 (1)根据题意和表格中的数据可以得到y关于x的函数关系式;
(2)根据题意可以的相应的不等式,再根据(1)中的函数关系式即可解答本题.
解答 解:(1)由题意可得,
y=(3-2.4)x+(2.5-2)(30-x)=0.1x+15,
即y关于x的函数关系式是y=0.1x+15;
(2)由题意可得,
2.4x+2(30-x)≤70,
解得,x≤25,
∵y=0.1x+15,
∴当x=25时,y取得最大值,此时y=17.5,30-x=5,
答:要使获得的收益最大,基地应种植郁金香25亩,玫瑰5亩.
点评 本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和不等式的性质解答.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
6.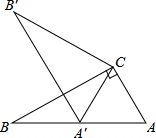 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )| A. | 150° | B. | 90° | C. | 60° | D. | 30° |
7.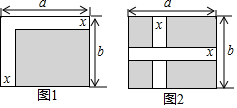 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )| A. | a(b-x)=ab-ax | B. | b(a-x)=ab-bx | ||
| C. | (a-x)(b-x)=ab-ax-bx | D. | (a-x)(b-x)=ab-ax-bx+x2 |
4.在下列所给的坐标的点中,在第二象限的是( )
| A. | (1,-2) | B. | (-1,-4) | C. | (-2,5) | D. | (0,1) |
11.甲、乙、丙三地海拔高度分别为-100米、-300米、500米,那么最高的地方比最低的地方高( )
| A. | 400米 | B. | 600米 | C. | 200米 | D. | 800米 |
1.某校有15名同学参加某比赛,预赛成绩各不相同,取前8名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这15名同学成绩的( )
| A. | 最高分 | B. | 中位数 | C. | 方差 | D. | 平均数 |
8.今年秋季,我县县城部分学校将准备搬迁新校舍,在迁入新校舍之前,某学校的同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了表格,条形图和扇形统计图,请你根据图表信息完成下列各题:
(1)此次共调查了多少位学生?
(2)请将表格填充完整;
(3)请将条形统计图补充完整.
(4)如果该校共有1000名学生,请你计算该校步行和骑自行车的一共有多少人?
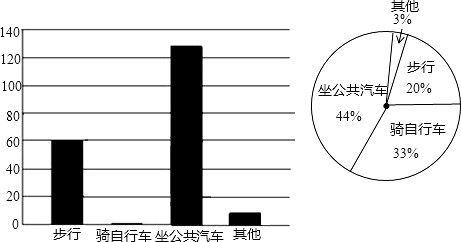
(1)此次共调查了多少位学生?
(2)请将表格填充完整;
| 步行 | 骑自行车 | 坐公共汽车 | 其他 |
| 60 |
(4)如果该校共有1000名学生,请你计算该校步行和骑自行车的一共有多少人?

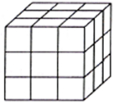 如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;