题目内容
7.计算:(1)$\frac{2}{{a}^{2}-4}$•($\frac{{a}^{2}+4}{4a}$-1)÷($\frac{1}{2}$-$\frac{1}{a}$)
(2)($\frac{x+y}{x-y}$)•$\frac{2y-2x}{3x+3y}$-$\frac{{x}^{2}}{{x}^{2}-{y}^{2}}$÷$\frac{x}{y}$.
分析 (1)先对括号内的式子化简,然后根据分式的乘除进行计算即可解答本题;
(2)先算乘除,再算减法即可解答本题.
解答 解:(1)$\frac{2}{{a}^{2}-4}$•($\frac{{a}^{2}+4}{4a}$-1)÷($\frac{1}{2}$-$\frac{1}{a}$)
=$\frac{2}{(a-2)(a+2)}$•$\frac{{a}^{2}+4-4a}{4a}$÷$\frac{a-2}{2a}$
=$\frac{2}{(a-2)(a+2)}•\frac{(a-2)^{2}}{4a}×\frac{2a}{a-2}$
=$\frac{1}{a+2}$;
(2)($\frac{x+y}{x-y}$)•$\frac{2y-2x}{3x+3y}$-$\frac{{x}^{2}}{{x}^{2}-{y}^{2}}$÷$\frac{x}{y}$
=$\frac{x+y}{x-y}•\frac{2(y-x)}{3(x+y)}-\frac{{x}^{2}}{(x+y)(x-y)}×\frac{y}{x}$
=$-\frac{2}{3}-\frac{xy}{{x}^{2}-{y}^{2}}$
=$-\frac{2{x}^{2}-2{y}^{2}+3xy}{3({x}^{2}-{y}^{2})}$.
点评 本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算方法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.下列运算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | (3xy2)2=6x2y4 | C. | a3•a2=a5 | D. | ($\sqrt{2}+1$)($1-\sqrt{2}$)=1 |
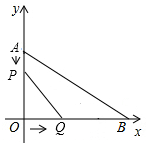 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.