题目内容
15.解方程:$\frac{2x}{x+1}-\frac{3}{{{x^2}-1}}=2$.分析 首先方程的两边同乘以最简公分母(x+1)(x-1),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.
解答 解:方程两边同乘(x+1)(x-1),
得:2x(x-1)-3=2(x+1)(x-1),
解得:x=-$\frac{1}{2}$,
经检验:x=-$\frac{1}{2}$是原方程的解;
因此原方程的解为x=-$\frac{1}{2}$.
点评 本题主要考查解分式方程,关键在于“转化思想”,把分式方程转化为整式方程求解,最后一定注意要验根.

练习册系列答案
相关题目
5.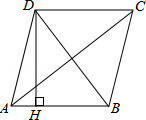 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 4 | D. | 8 |
6.${(-\frac{3}{2})^{-2}}$的结果为( )
| A. | $\frac{9}{4}$ | B. | $-\frac{4}{9}$ | C. | $\frac{4}{9}$ | D. | $-\frac{9}{4}$ |
3.下列计算中,错误的是( )
| A. | 5a3-a3=4a3 | B. | 2n•3n=6n+n | C. | (a-b)3•(b-a)2=(a-b)5 | D. | -a2•(-a)3=a5 |
10.要使分式$\frac{x}{x-2}$有意义,则x应满足的条件是( )
| A. | x<2 | B. | x≠2 | C. | x≠0 | D. | x>2 |
5.在下列各数-(+3)、-22、(-2)2、(-1)2015、-|-4|中,负数有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 某市有A,B,C,D,E五个景点,该市旅游局对某月进入景点的人数的情况进行调查统计,并将统计结果绘制成如图所示的两幅不完整的统计图.
某市有A,B,C,D,E五个景点,该市旅游局对某月进入景点的人数的情况进行调查统计,并将统计结果绘制成如图所示的两幅不完整的统计图.