题目内容
7.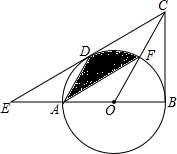 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
分析 (1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.
(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.
解答 (1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DOC=∠BOC,
在△CDO和△CBO中,\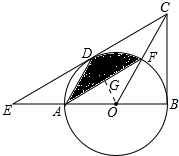 $\left\{\begin{array}{l}{CO=CO}\\{∠DOC=∠BOC}\\{OD=OB}\end{array}\right.$,
$\left\{\begin{array}{l}{CO=CO}\\{∠DOC=∠BOC}\\{OD=OB}\end{array}\right.$,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线.
(2)由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,
∴∠DCO=∠BCO=$\frac{1}{2}$∠ECB=30°,
∴∠DOC=∠BOC=60°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,
$\left\{\begin{array}{l}{∠GOF=∠ADG}\\{∠FGO=∠AGD}\\{AD=OF}\end{array}\right.$,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF=$\frac{60π•{3}^{2}}{360}$=$\frac{3}{2}$π.
点评 本题考查切线的性质和判定、扇形的面积公式,记住切线的判定方法和性质是解决问题的关键,学会把求不规则图形面积转化为求规则图形面积,属于中考常考题型.

练习册系列答案
相关题目
19.初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖,如图:
那么被遮盖的两个数据依次是( )
| 编号 | 1 | 2 | 3 | 4 | 5 | 方差 | 平均成绩 |
| 得分 | 38 | 34 | ■ | 37 | 40 | ■ | 37 |
| A. | 35,2 | B. | 36,4 | C. | 35,3 | D. | 36,3 |
16.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.
如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B. 如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3. 解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来.
解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来. 在数轴上表示实数a的点如图所示,化简$\sqrt{{{(a-5)}^2}}$+|a-2|的结果为3.
在数轴上表示实数a的点如图所示,化简$\sqrt{{{(a-5)}^2}}$+|a-2|的结果为3.