题目内容
15.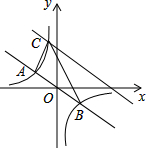 如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.(1)求反比例函数的表达式;
(2)将直线y=-$\frac{1}{2}$x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
分析 (1)将y=3代入一次函数解析式中,求出x的值,即可得出点A的坐标,再利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式;
(2)平移后直线于y轴交于点F,连接AF、BF,设平移后的解析式为y=-$\frac{1}{2}$x+b,由平行线的性质可得出S△ABC=S△ABF,结合正、反比例函数的对称性以及点A的坐标,即可得出关于b的一元一次方程,解方程即可得出结论.
解答 解:(1)令一次函数y=-$\frac{1}{2}$x中y=3,则3=-$\frac{1}{2}$x,
解得:x=-6,即点A的坐标为(-6,3).
∵点A(-6,3)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-6×3=-18,
∴反比例函数的表达式为y=-$\frac{18}{x}$.
(2)设平移后直线于y轴交于点F,连接AF、BF如图所示.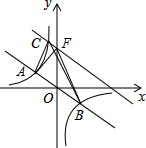
设平移后的解析式为y=-$\frac{1}{2}$x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为48,
∴S△ABF=$\frac{1}{2}$OF•(xB-xA)=48,
由对称性可知:xB=-xA,
∵xA=-6,
∴xB=6,
∴$\frac{1}{2}$b×12=48,
∴b=8.
∴平移后的直线的函数表达式为y=-$\frac{1}{2}$x+8.
点评 本题考查了反比例函数与一次函数交点的问题、反比例函数图象上点的坐标特征.三角形的面积公式以及平行线间的距离公式,解题的关键是:(1)求出点A的坐标;(2)找出关于b的一元一次方程.本题属于中档题,难度不大,解决该题型题目时,巧妙的利用面积法要比找相似三角形简单明了的多.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
13.下列说法中,不正确的是( )
| A. | 垂线段最短 | B. | 两直线平行,同旁内角相等 | ||
| C. | 对顶角相等 | D. | 两点之间,线段最短 |
 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.

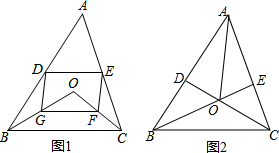 点D,E分别是△ABC的边AB,AC的中点.
点D,E分别是△ABC的边AB,AC的中点.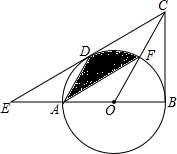 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.
如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.