题目内容
5.某花店专卖某种进口品种的月季花苗,购进时每盆花苗的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600盆,而销售单价每上涨1元,就会少售出10盆.(1)设该种月季花苗的销售单价在40元的基础上涨了x元(x>0),若要使得花店每盆的利润不得低于14元,且花店要完成不少于540盆的销售任务,求x的取值范围;
(2)在(1)问前提下,若设花店所获利润为W元,试用x表示W,并求出当销售单价为多少时W最大,最大利润是什么?
分析 (1)利用“花店每盆的利润不得低于14元,且花店要完成不少于540盆的销售任务”进而得出不等式组求出x的取值范围;
(2)首先得出W与x之间的函数关系式,再利用二次函数性质求出最值即可.
解答 解:(1)由题意可得:
涨价后的销量为:600-10x,
则$\left\{\begin{array}{l}{x≥4}\\{600-10x≥540}\end{array}\right.$,
解得:4≤x≤6,
故x的取值范围为:4≤x≤6;
(2)由题意可得:
W=(x+10)(600-10x)
=-10x2+500x+6000
∵4≤x≤6,
∴当x=6时W最大,即售价为:40+6=46(元)时,
W最大=-10×62+500×6+6000=8640(元),
答:当销售单价为46时W最大,最大利润是8640元.
点评 此题主要考查了二次函数的应用以及不等式组的应用,根据题意得出x的取值范围是解题关键.

练习册系列答案
相关题目
13.下列说法中,不正确的是( )
| A. | 垂线段最短 | B. | 两直线平行,同旁内角相等 | ||
| C. | 对顶角相等 | D. | 两点之间,线段最短 |
20.如图,三个图形是由立体图形展开得到的,相应的立体图形顺序是( )


| A. | 圆柱、三棱柱、圆锥 | B. | 圆锥、三棱柱、圆柱 | ||
| C. | 圆柱、三棱锥、圆锥 | D. | 圆柱、三棱柱、半球 |
10.小雨找了四根木条,长度分别是3cm、8cm,10cm、11cm,他想选择其中三根组成一个三角形,可能的选法有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
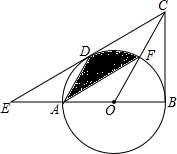 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.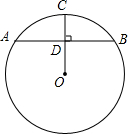 如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.
如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.