题目内容
17. 如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.
如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.(1)求弦AB的长度;
(2)计算S△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).
分析 (1)OA和AB的长度是一元二次方程的根,所以利用韦达定理即可求出AB的长度.
(2)作出△AOB的高OC,然后求出OC的长度即可.
(3)由题意知:两三角形有公共的底边,要面积相等,即高要相等.
解答 解:(1)由题意知:OA和AB的长度是x2-4x+a=0的两个实数根,
∴OA+AB=-$\frac{-4}{1}$=4,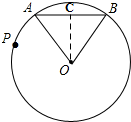
∵OA=2,
∴AB=2;
(2)过点C作OC⊥AB于点C,
∵OA=AB=OB=2,
∴△AOB是等边三角形,
∴AC=$\frac{1}{2}$AB=1
在Rt△ACO中,
由勾股定理可得:OC=$\sqrt{3}$
∴S△AOB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$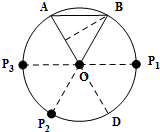 (3)延长AO交⊙O于点D,
(3)延长AO交⊙O于点D,
由于△AOB与△POA有公共边OA,
当S△POA=S△AOB时,
∴△AOB与△POA高相等,
由(2)可知:等边△AOB的高为$\sqrt{3}$,
∴点P到直线OA的距离为$\sqrt{3}$,这样点共有3个
①过点B作BP1∥OA交⊙O于点P1,
∴∠BOP1=60°,
∴此时点P经过的弧长为:$\frac{240°π×2}{180°}$=$\frac{8π}{3}$,
②作点P2,使得P1与P2关于直线OA对称,
∴∠P2OD=60°,
∴此时点P经过的弧长为:$\frac{120°π×2}{180°}$=$\frac{4}{3}$π,
③作点P3,使得B与P3关于直线OA对称,
∴∠P3OP2=60°,
∴此时P经过的弧长为:$\frac{60°π×2}{180°}$=$\frac{2π}{3}$,
综上所述:当S△POA=S△AOB时,P点所经过的弧长分别是$\frac{4}{3}π$、$\frac{8}{3}π$、$\frac{2π}{3}$.
点评 此题考查了一元二次方程与圆的综合知识.涉及等边三角形性质,圆的对称性等知识,对学生综合运用知识的能力要求较高.故要求学生把所学知识融汇贯穿,灵活运用.

| A. | a=9 b=12 c=15 | B. | a=32 b=42 c=52 | C. | a=12 b=18 c=22 | D. | a:b:c=1:1:2 |
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
| A. | 必然事件的概率为1 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的方差为8.5 | |
| D. | 若某抽奖活动的中奖率为40%,则参加这种活动10次必有4次中奖 |
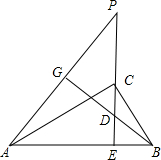 如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE.
如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE. 函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集
函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集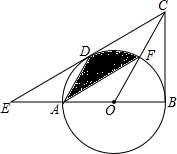 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.