题目内容
5.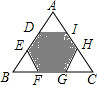 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
分析 根据正六边形的每一个内角是120°得到△ADI是等边三角形,得到$\frac{AD}{AB}$=$\frac{1}{3}$,根据相似三角形的性质得到S△ADI=$\frac{1}{9}$S△ABC,计算即可.
解答 解:∵六边形DEFGHI是正六边形,
∴∠EDI=120°,
∴∠ADI=60°,
∴△ADI是等边三角形,
∴AD=DE,
同理,BE=DE,
∴AD=DE=EB,
∴$\frac{AD}{AB}$=$\frac{1}{3}$,
∴S△ADI=$\frac{1}{9}$S△ABC,
同理S△BEF=$\frac{1}{9}$S△ABC,S△CGH=$\frac{1}{9}$S△ABC,
∴$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=$\frac{2}{3}$,
故选:C.
点评 本题考查的是正多边形和圆,掌握正多边形的概念和性质以及相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 平角是一条直线 | B. | 角的边越长,角越大 | ||
| C. | 大于直角的角叫做钝角 | D. | 两个锐角的和不一定是钝角 |
17.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )
| A. | ab=1 | B. | a+b=0 | C. | a-b=0 | D. | a2=b2 |
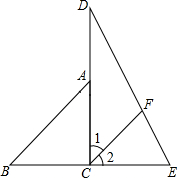 将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
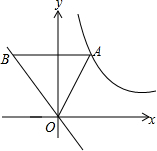 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.