题目内容
3.已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是等腰三角形;若三角形的两边长为3和5,第三边长是偶数,则第三边长可以是4或6.分析 (1)根据三角形的内角和定理,求出第三个角,再判断三角形的形状.
(2)能够根据三角形的三边关系“第三边应等于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是偶数这一条件,求得第三边的值即可.
解答 解:
(1)第三个角是180°-40°-70°=70°,
则三角形是等腰三角形;
故答案为:等腰三角形;
(2)由题意,令第三边为x,则5-3<x<5+3,即2<x<8,
∵第三边长为偶数,
∴第三边长是4或6
故答案为:4或6.
点评 (1)此考查了三角形的内角和定理以及等腰三角形的定义,熟记三角形内角和定理是解题关键.
(2)此题主要考查了三角形三边关系,熟练掌握三角形的三边关系是解决此类问题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
13.下列说法正确的是( )
| A. | 平角是一条直线 | B. | 角的边越长,角越大 | ||
| C. | 大于直角的角叫做钝角 | D. | 两个锐角的和不一定是钝角 |
8.小明同学在计算某n边形的内角和时,不小心多输入一个内角,得到和为2005°,则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
13.下列计算中,正确的是( )
| A. | 2×2-2=$\frac{1}{2}$ | B. | (-9)0=-1 | C. | 3a-2=$\frac{1}{3{a}^{2}}$(a≠0) | D. | a5×a-3=a5÷a3 |
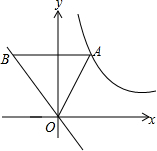 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.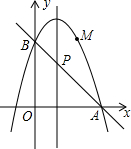 已知二次函数y=-x2+2x+m
已知二次函数y=-x2+2x+m