题目内容
9.瑶海教育局计划在3月12日植树节当天安排A,B两校部分学生到郊区公园参加植树活动.已知A校区的每位学生往返车费是6元,B校每位学生的往返车费是10元,要求两所学校均要有学生参加,且A校参加活动的学生比B校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求A,B两校最多各有多少学生参加?分析 设A校有x名学生参加,B校有(x+4)名学生参加,根据往返车费=单人费用×人数,可列出关于x的一元一次不等式,解不等式可得出x的取值范围,从而得出结论.
解答 解:设A校有x名学生参加,B校有(x+4)名学生参加,依题意得
6x+10(x+4)≤210,解得:x≤10$\frac{5}{8}$.
∵x为整数,
∴x最多为10,x+4=10+4=14.
答:A校最多有10名学生参加,B校最多有14名学生参加.
点评 本题考查了一元一次不等式的应用,解题的关键是根据数量关系列出一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出一元一次不等式(或不等式组)是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )
| A. | ab=1 | B. | a+b=0 | C. | a-b=0 | D. | a2=b2 |
1.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
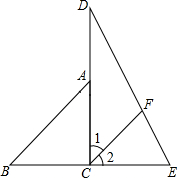 将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.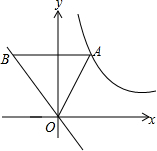 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.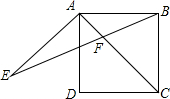 如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.
如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.