题目内容
由于受到手机更新换代的影响,某品牌第一代手机二月售价比一月每台降价500元.如果卖出相同数量的一代手机,那么一月销售额为4.5万元,二月销售额只有4万元.
(1)一月第一代手机每台售价为多少元?
(2)为了提高利润,该店计划三月购进部分第二代手机销售,已知第一代手机每台进价为3500元,第二代手机每台进价为4000元,预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机共20台,请问有哪几种进货方案?
(3)该店计划4月对第一代手机的尾货进行销售,决定在二月售价基础上每售出一台第一代手机再返还顾客现金a元,而第二代手机按销售价4400元销售,如要使(2)中所有方案获利相同,a应取何值?
(1)一月第一代手机每台售价为多少元?
(2)为了提高利润,该店计划三月购进部分第二代手机销售,已知第一代手机每台进价为3500元,第二代手机每台进价为4000元,预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机共20台,请问有哪几种进货方案?
(3)该店计划4月对第一代手机的尾货进行销售,决定在二月售价基础上每售出一台第一代手机再返还顾客现金a元,而第二代手机按销售价4400元销售,如要使(2)中所有方案获利相同,a应取何值?
考点:分式方程的应用,一元一次不等式组的应用
专题:
分析:(1)设一月第一代手机每台售价为x元,则二月一代手机每台售价为(x-500)元,根据关键语句“卖出相同数量的一代手机”可得:
=
,再解方程即可;
(2)设三月购进一代手机y台,购进二代手机(20-y)台.根据关键语句“预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机”得:74000≤一代手机每台进价×数量+二代手机每台进价×数量≤75000,有由不等关系列出不等式,解不等式即可;
(3)设总获利W元,根据题意得等量关系:W=每台一代手机获利×台数+每台二代手机获利×台数,由等量关系可得方程:[(4500-500-a)-3500]y+(4400-4000)(20-y)整理以后使的y系数等于0即可.
| 45000 |
| x |
| 40000 |
| x-500 |
(2)设三月购进一代手机y台,购进二代手机(20-y)台.根据关键语句“预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机”得:74000≤一代手机每台进价×数量+二代手机每台进价×数量≤75000,有由不等关系列出不等式,解不等式即可;
(3)设总获利W元,根据题意得等量关系:W=每台一代手机获利×台数+每台二代手机获利×台数,由等量关系可得方程:[(4500-500-a)-3500]y+(4400-4000)(20-y)整理以后使的y系数等于0即可.
解答:(1)解:设一月第一代手机每台售价为x元,则二月一代手机每台售价为(x-500)元,
=
,
解得,x=4500
经检验:x=4500是原方程的解
答:一月一代4手机每台售价为4500元;
(2)设三月购进一代手机y台,购进二代手机(20-y)台.74000≤3500y+4000(20-y)≤7500010≤y≤12
∵y是正整数,∴y=10,11,12
∴共有三种进货方案:一代手机10台,二代手机10台;
一代手机11台,二代手机9台;
一代手机12台,二代手机8台;
(3)[(4500-500-a)-3500]y+(4400-4000)(20-y)
∵要使(2)中所有方案获利相同,
∴取值与y无关,
∴a=100.
| 45000 |
| x |
| 40000 |
| x-500 |
解得,x=4500
经检验:x=4500是原方程的解
答:一月一代4手机每台售价为4500元;
(2)设三月购进一代手机y台,购进二代手机(20-y)台.74000≤3500y+4000(20-y)≤7500010≤y≤12
∵y是正整数,∴y=10,11,12
∴共有三种进货方案:一代手机10台,二代手机10台;
一代手机11台,二代手机9台;
一代手机12台,二代手机8台;
(3)[(4500-500-a)-3500]y+(4400-4000)(20-y)
|
∵要使(2)中所有方案获利相同,
∴取值与y无关,
∴a=100.
点评:此题主要考查了分式方程的应用,一元一次不等式组的应用,一次函数的应用,是一道综合题,关键是弄清题意,找出题目中的等量关系与不等关系,列出方程与不等式组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=
如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=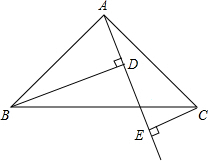 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问: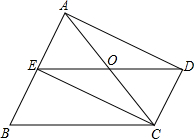 已知:如图,DC∥AB,且DC=AE,E为AB的中点,
已知:如图,DC∥AB,且DC=AE,E为AB的中点,