题目内容
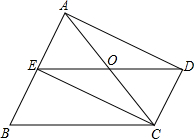 已知:如图,DC∥AB,且DC=AE,E为AB的中点,
已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.
(2)观察图形,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):
考点:全等三角形的判定与性质
专题:
分析:(1)由DC∥AB,且DC=
AB,E为AB的中点,可判定四边形ADCE是平行四边形,有CE=AD,CE∥AD?∠BEC=∠BAD,故可由SAS证得△BEC≌△EAD,在
(2)平行四边形ADCE中,△AED,△AEC,△ECD,△AED都是等底等高的三角形,故它们的面积相等.
| 1 |
| 2 |
(2)平行四边形ADCE中,△AED,△AEC,△ECD,△AED都是等底等高的三角形,故它们的面积相等.
解答:(1)证明:∵DC=AE,
∴DC=
AB,
∵E为AB的中点,
∴CD=BE=AE.
又∵DC∥AB,
∴四边形ADCE是平行四边形.
∴CE=AD,CE∥AD.
∴∠BEC=∠BAD.
在△BEC和△EAD中,
,
∴△BEC≌△EAD(SAS).
(2)解:与△AED的面积相等的三角形有:△AEC,△ECD,△AED.
故答案为:△AEC,△ECD,△ACD.
∴DC=
| 1 |
| 2 |
∵E为AB的中点,
∴CD=BE=AE.
又∵DC∥AB,
∴四边形ADCE是平行四边形.
∴CE=AD,CE∥AD.
∴∠BEC=∠BAD.
在△BEC和△EAD中,
|
∴△BEC≌△EAD(SAS).
(2)解:与△AED的面积相等的三角形有:△AEC,△ECD,△AED.
故答案为:△AEC,△ECD,△ACD.
点评:本题考查了全等三角形的判定和性质;三角形全等的判定是中考的热点,一般以考查三角形全等的方法SSS、SAS、ASA、AAS、HL为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 如图,经过原点的抛物线y=-2x2+4x与x轴的另一个交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C,D两点,与原抛物线交于点P.
如图,经过原点的抛物线y=-2x2+4x与x轴的另一个交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C,D两点,与原抛物线交于点P. 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面、左面看到的这个几何体的形状图.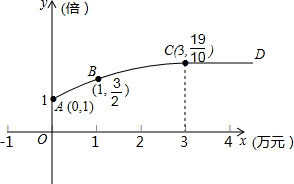 某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费
某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费 如图,在方格纸上的每一个格点处放一枚棋子,共放16枚棋子,求以棋子为顶点的正方形的个数.
如图,在方格纸上的每一个格点处放一枚棋子,共放16枚棋子,求以棋子为顶点的正方形的个数.