题目内容
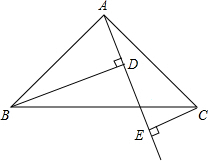 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:(1)AD与CE的大小关系如何?请说明理由.
(2)你能说明DE=BD-CE的理由吗?
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)AD=CE,由已知可得AB=AC,∠BDA=∠AEC=90°,∠BAD=∠ACE;两角及其一角的对边对应相等的两个三角形全等,利用△ABD≌△CAE即可得到AD=CE;
(2)据△ABD≌△CAE,可得BD=AE,AD=EC,又AE=AD+DE,故可得BD=DE+CE,即DE=BD-CE.
(2)据△ABD≌△CAE,可得BD=AE,AD=EC,又AE=AD+DE,故可得BD=DE+CE,即DE=BD-CE.
解答:解:(1)AD=CE,
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
又∵BD⊥AE,
∴∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AD=CE;
(2)证明:∵△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=DE+AD,
∴BD=DE+CE,
∴DE=BD-CE.
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
又∵BD⊥AE,
∴∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AD=CE;
(2)证明:∵△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=DE+AD,
∴BD=DE+CE,
∴DE=BD-CE.
点评:本题考查了直角三角形的边角关系,全等三角形的判定和性质等知识点,属中档题,做题时要从已知开始,结合相关知识认真思考.

练习册系列答案
相关题目
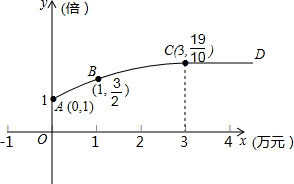 某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费
某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费 如图,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°,求∠C和∠D.
如图,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°,求∠C和∠D.