题目内容
18．
如图，在△ABC中，AB=3，AC=4，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是（ ）| A． | 7 | B． | 6 | C． | 5 | D． | 4 |
分析 根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可．
解答 
解：在△ABC中，AB=3，AC=4，BC=5，
∴AB2+AC2=BC2，
∴∠BAC=90°
∵EF垂直平分BC，
∴B、C关于EF对称，
AC交EF于D，
∴当P和D重合时，AP+BP的值最小，最小值等于AC的长，
由勾股定理得：AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4．
故选D．
点评 本题考查了勾股定理的逆定理，勾股定理，轴对称-最短路线问题的应用，解此题的关键是找出P的位置．
练习册系列答案
相关题目
如图，直线y=kx-4（k＞0）与双曲线y=$\frac{k}{x}$在第一象限内交于点R，与x，y轴的交点分别为P，Q；过R作RM⊥x轴，M为垂足，若△OPQ与△PRM的面积相等，则k的值等于4$\sqrt{2}$．
9．下列多项式相乘，不能用平方差公式计算的是（ ）
| A． | （x-2y）（2y+x） | B． | （2y-x）（-x-2y） | C． | （x-2y）（-x-2y） | D． | （-2y-x）（x+2y） |
如图所示，△DEF是等边三角形，且∠1=∠2=∠3，试问：△ABC是等边三角形吗？请说明理由．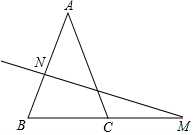
已知：如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．
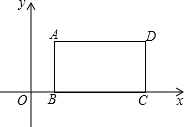如图，长方形ABCD在直角坐标系中，边BC在x轴上，B点坐标为（m，0）且m＞0．AB=a，BC=b，且满足b=$\sqrt{3-a}$-$\sqrt{a-3}$+4