题目内容
8. 如图,直线y=kx-4(k>0)与双曲线y=$\frac{k}{x}$在第一象限内交于点R,与x,y轴的交点分别为P,Q;过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于4$\sqrt{2}$.
如图,直线y=kx-4(k>0)与双曲线y=$\frac{k}{x}$在第一象限内交于点R,与x,y轴的交点分别为P,Q;过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于4$\sqrt{2}$.
分析 分别将x=0、y=0代入一次函数解析式求出与之对应的y、x值,由此即可得出点Q、P的坐标,再根据RM⊥x轴结合公共角∠OPQ=∠MPR即可得出△OPQ∽△MPR,结合两三角形面积相等即可得出△OPQ≌△MPR,依据全等三角形的性质即可得出点R的坐标,将其代入反比例函数解析式中即可得出关于k的分式方程,解之即可得出结论.
解答 解:当x=0时,y=kx-4=-4,
∴点Q(0,-4);
当y=kx-4=0时,x=$\frac{4}{k}$,
∴点P($\frac{4}{k}$,0).
∵RM⊥x轴,
∴∠POQ=∠PMR=90°.
又∵∠OPQ=∠MPR,
∴△OPQ∽△MPR.
∵△OPQ与△PRM的面积相等,
∴△OPQ≌△MPR,
∴OP=MP,OQ=MR,
∴点R($\frac{8}{k}$,4).
∵点R在双曲线y=$\frac{k}{x}$上,
∴4=$\frac{k}{\frac{8}{k}}$,解得:k=4$\sqrt{2}$或k=-4$\sqrt{2}$(舍去).
经检验,k=4$\sqrt{2}$是方程4=$\frac{k}{\frac{8}{k}}$的解.
故答案为:4$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征、相似三角形的判定、全等三角形的性质以及反比例函数图象上点的坐标特征,根据全等三角形的性质找出点R的坐标是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
17. 如图所示的平面图形绕轴旋转一周,可得到的立体图形是( )
如图所示的平面图形绕轴旋转一周,可得到的立体图形是( )
 如图所示的平面图形绕轴旋转一周,可得到的立体图形是( )
如图所示的平面图形绕轴旋转一周,可得到的立体图形是( )| A. | 圆锥 | B. | 圆柱 | C. | 三棱锥 | D. | 棱柱 |
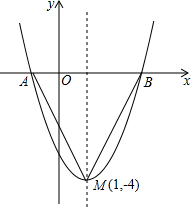 如图:二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图:二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4). 如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.
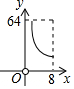
如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.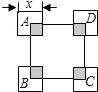 如图,大正方形ABCD的边长为8,四个全等的小正方形的对称中心分别在大正方形的四个顶点上,且它们的各边与正方形各边平行或垂直.若小正方形的边长为(0<x≤8),重叠部分的面积为y,能反映y与x之间函数关系的大致图象是( )
如图,大正方形ABCD的边长为8,四个全等的小正方形的对称中心分别在大正方形的四个顶点上,且它们的各边与正方形各边平行或垂直.若小正方形的边长为(0<x≤8),重叠部分的面积为y,能反映y与x之间函数关系的大致图象是( )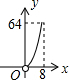
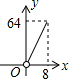

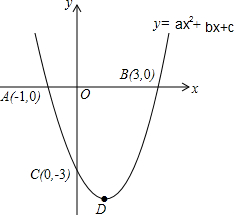 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点. 如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )
如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )