题目内容
3.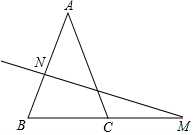 已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其他条件不变,再求∠NMB的度数;
(3)通过对(1)中和(2)中结果的分析,猜想∠NMB的度数与∠A的度数有怎样的等量关系?并证明你的结论.
分析 (1)先根据等腰三角形的性质得出∠B的度数,再由直角三角形的性质即可得出结论;
(2)解法同(1);
(3)设∠A=α,根据AB=AC可知∠B=∠C,再由直角三角形的性质即可得出结论.
解答 解:(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-40°)=70°,
∴∠NMB=90°-∠B=90°-70°=20°;
(2)解法同(1),可得∠NMB=35°;
(3)两者关系为:∠NMB的度数等于顶角∠A度数的一半,
证明:设∠A=α,
∵AB=AC,
∴∠B=∠C,
∴∠B=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-α),
∵∠BNM=90°,
∴∠NMB=90°-∠B=90°-$\frac{1}{2}$(180°-α)=$\frac{1}{2}$α.
点评 本题考查的是等腰三角形的性质,线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
8.已知点P在△ABC内,若AP=CP,且AB>BC,则点P一定在( )
| A. | 边AC的垂直平分线上 | B. | 边AB的垂直平分线上 | ||
| C. | 边BC的垂直平分线上 | D. | 边AC的高上 |
15.下列说法正确的是( )
| A. | -8是64的平方根 | B. | $\sqrt{2}$的算术平方根是2 | ||
| C. | 0没有算术平方根 | D. | 2的平方根是 $\sqrt{2}$ |
12.某超市的老板对2016年1-3月该超市每个月的利润进行统计,其统计结果如表所示,盈利用正数表示,亏损用负数表示,则该超市2016年1-3月份的总利润为( )
| 月份 | 1月 | 2月 | 3月 |
| 利润/万元 | +1.2 | -0.5 | +1.5 |
| A. | 2.7万元 | B. | 2.2万元 | C. | 1.9万元 | D. | 1.7万元 |
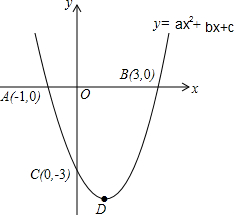 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.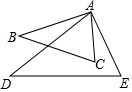 如图,在△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,求∠CAE的度数.
如图,在△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,求∠CAE的度数. 如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )
如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )