题目内容
19.(1)计算:($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$);(2)计算(2$\sqrt{3}$-$\sqrt{6}$)2+($\sqrt{54}$+2$\sqrt{6}$)÷$\sqrt{3}$.
分析 (1)先把各二次根式化为最简二次根式,然后去括号合并即可;
(2)先进行二次根式的乘除法运算,然后合并即可.
解答 解:(1)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$
=$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$;
(2)原式=12-12$\sqrt{2}$+6+$\sqrt{54÷3}$+2$\sqrt{6÷3}$
=18-12$\sqrt{2}$+3$\sqrt{2}$+2$\sqrt{2}$
=18-7$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
7.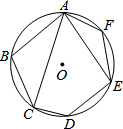 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )| A. | 220° | B. | 240° | C. | 260° | D. | 280° |
14. 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
 如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )
如图,平行四边形ABCD中,AE平分∠DAB,∠B=110°,则∠DEA等于( )| A. | 110° | B. | 80° | C. | 55° | D. | 35° |
 …,请仔细观察,按此规律在前8个图案中有2个
…,请仔细观察,按此规律在前8个图案中有2个 ,按此规律在前15个图案中有4个
,按此规律在前15个图案中有4个 ,按此规律在前2015个图案中有503个
,按此规律在前2015个图案中有503个
 如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.
如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.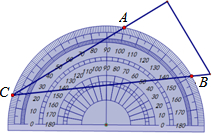 将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A、B的读数分别为100°、150°,则∠ACB的大小为25度.
将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A、B的读数分别为100°、150°,则∠ACB的大小为25度.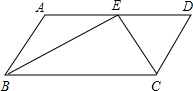 已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.
已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.