题目内容
9.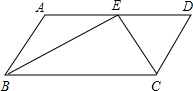 已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.
已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.
分析 根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=17.根据等腰三角形的性质得到AB=CD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
解答 解:(1)∵BE和CE分别平分∠ABC和∠BCD,
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴$\frac{1}{2}$(∠ABC+∠DCB)=90°,
∴∠EBC+∠ECB=90°,
∴△EBC是直角三角形,
根据勾股定理:BC=17,
∵AD∥BC,
∴∠DEC=∠ECB,
∵∠ECD=∠ECB,
∴∠DEC=∠ECD,
∴DE=CD,
同理AB=AE.
∴AB+CD=AE+DE=AD=BC=17,
∴平行四边形ABCD周长=BC+AD+AB+CD=17+17+17=51.
(2)如图,作EH⊥BC,垂足为H.
S△BEC=$\frac{1}{2}$×15×8=60,
又∵S△BEC=$\frac{1}{2}$×BC×EH,
∴S平行四边形ABCD=BC×EH=2S△BEC=120.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
相关题目
20.为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如表:
气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的水注入小明家的蓄水池?
| 小明家 | 爷爷家 | |
| 屋顶收集雨水面积(m2) | 160 | 120 |
| 蓄水池容积(m3) | 50 | 13 |
| 蓄水池已有水量(m3) | 34 | 11.5 |
1.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
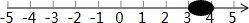 把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.
把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.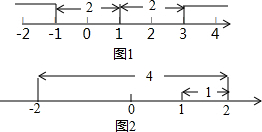
 ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( ) <
< B.
B. 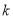 <2 C.
<2 C. 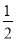 <
<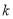 <2 D.
<2 D. 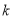 >2
>2