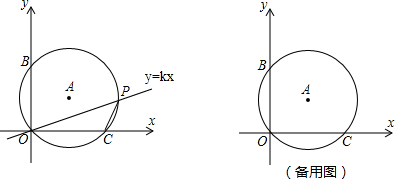题目内容
6.如图①,在平面直角坐标系xoy的第一象限中,有一个Rt△OAB,∠B=90°,OB=3,AB=4,点A在正半轴上,⊙I是Rt△OAB的内切圆.①求点B的坐标.
②求内心I的坐标.
③将⊙I平移,使内心I与点B重合,如图②,点P是x轴正半轴上一点,是否存在⊙P同时与y轴、⊙B相切?若存在,求出点P的坐标;若不存在,请说明理由.

分析 ①如图①,过点B作BC⊥OA于C,在Rt△OAB中,根据勾股定理可得OA=5,根据三角形面积公式可得BC=2.4,在Rt△OBC中,根据勾股定理可得OC,从而得到B(1.8,2.4);
②如图①b,设切点分别为D、E、F,连接ID、IE、IF,根据切线的性质可得四边形BEIF是正方形,设ID=x,则BE=BF=x,列出方程(3-x)+(4-x)=5,解得x,进一步得到I的坐标为(2,1);
③如图②,设OP=x,分两种情况:(1)如图②a,当x为半径的⊙P与⊙B相外切时;(2)如图②b,当x为半径的⊙P与⊙B相内切时;进行讨论即可求解.
解答 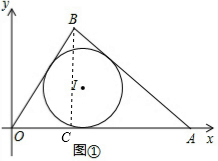 ①解:如图①,过点B作BC⊥OA于C,
①解:如图①,过点B作BC⊥OA于C,
∵Rt△OAB,∠B=90°,OB=3,AB=4,
∴OA=5,
∵S△OAB=$\frac{1}{2}×3×4=\frac{1}{2}×5×BC$,
∴BC=2.4,
Rt△OBC中,OC=$\sqrt{{3^2}-{{2.4}^2}}$=1.8,
∴B(1.8,2.4);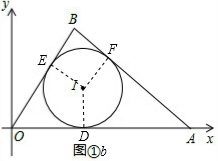 ②解:如图①b,设切点分别为D、E、F,连接ID、IE、IF,
②解:如图①b,设切点分别为D、E、F,连接ID、IE、IF,
则ID=IE=IF,BE=BF,OD=OE,AD=AF,且四边形BEIF是正方形,
设ID=x,则BE=BF=x,
∴OD=OE=3-x,AD=AF=4-x,
∵(3-x)+(4-x)=5,
∴x=1,
∴OD=3-1=2,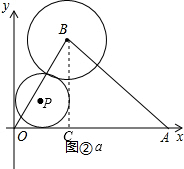 ∴I(2,1);
∴I(2,1);
③如图②,设OP=x,
∵OP⊥y轴,
∴以x为半径的⊙P与y轴相切;
(1)如图②a,当x为半径的⊙P与⊙B相外切时,有PB=x+1,
作BC⊥OA于C,则BC=2.4,PC=1.8-x,
2.42+(1.8-x)2=(x+1)2,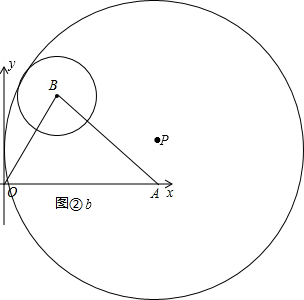 解得:$x=\frac{10}{7}$,
解得:$x=\frac{10}{7}$,
∴P($\frac{10}{7}$,0);
(2)如图②b,当x为半径的⊙P与⊙B相内切时,
∵AB+1=4+1=5=OA,
∴P与A点重合,
∴P(5.0).
综上所述,P点的坐标是($\frac{10}{7}$,0)或(5.0).
点评 本题考查了圆的综合题:熟练运用圆的切线性质和切线长定理进行几何证明;会运用勾股定理进行几何计算;同时考查了方程思想和分类思想的应用,综合性较强,难度较大.

| A. | 对角线互相垂直且平分的四边形是正方形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 四个角相等的四边形是矩形 | |
| D. | 一组对边平行另一组对边相等的四边是平行四边形 |
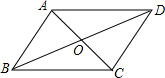 如图,在四边形ABCD中,对角线AC、BD相交于点O,∠ADB=∠CBD,AD=BC.
如图,在四边形ABCD中,对角线AC、BD相交于点O,∠ADB=∠CBD,AD=BC.