题目内容
20.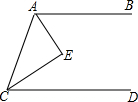 如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.
如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.
分析 先根据平行线的性质得出∠BAC+∠ACD=18°,再由角平分线的性质可得出∠EAC+∠ACE=90°,根据三角形内角和定理即可得出结论.
解答 解:∵AB∥CD,
∴∠BAC+∠ACD=180°.
∵∠BAC的平分线和∠ACD的平分线交于点E,
∴∠EAC+∠ACE=$\frac{1}{2}$(∠BAC+∠ACD)=90°,
∴∠AEC=180°-90°=90°,
∴AE与CE互相垂直.
故答案为:互相垂直.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
10.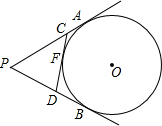 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )| A. | $\frac{2}{13}\sqrt{13}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
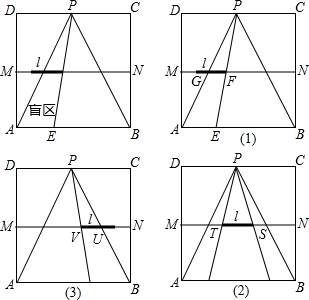
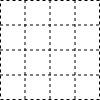 在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.
在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.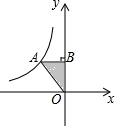 如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.
如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.