题目内容
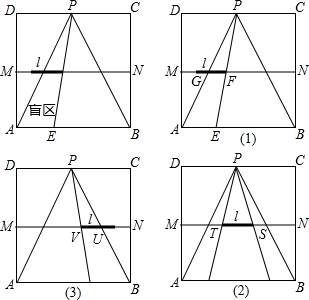
16.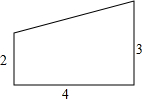 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
分析 根据题意,分两种情况讨论,求出每种情况下直角三角形的斜边的长度各是多少;然后用斜边的长度除以2,求出直角三角形的外接圆的半径是多少,即可求出能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是多少.
解答 解:(1)如图1,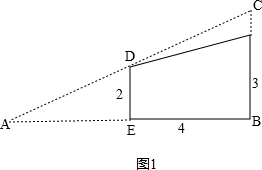 ,
,
当D、E分别是斜边AC、直角边AB的中点时,
∵D、E分别是斜边AC、直角边AB的中点,
∴$\frac{AE}{AB}=\frac{DE}{BC}=\frac{1}{2}$,
∴BC=2×2=4,AE=BE=4,AB=4+4=8,
∴AC=$\sqrt{{4}^{2}{+8}^{2}}=4\sqrt{5}$,
∴直角三角形ABC的外接圆的半径是:
4$\sqrt{5}÷2=2\sqrt{5}$,
即能刚好完全覆盖原直角三角形纸片的圆形纸片的半径是2$\sqrt{5}$.
(2)如图2,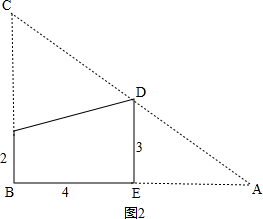 ,
,
当D、E分别是斜边AC、直角边AB的中点时,
∵D、E分别是斜边AC、直角边AB的中点,
∴$\frac{AE}{AB}=\frac{DE}{BC}=\frac{1}{2}$,
∴BC=3×2=6,AE=BE=4,AB=4+4=8,
∴AC=$\sqrt{{6}^{2}{+8}^{2}}=10$,
∴直角三角形ABC的外接圆的半径是:
10÷2=5,
即能刚好完全覆盖原直角三角形纸片的圆形纸片的半径是5.
综上,可得
能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
故答案为:2$\sqrt{5}$或5.
点评 (1)此题主要考查了图形的剪拼问题,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是求出原来直角三角形纸片的斜边的长度是多少.
(2)此题还考查了直角三角形的外接圆的半径的求法,要熟练掌握.

练习册系列答案
相关题目
6.甲、乙两农户是某农业合作社社员,他们今年种植了新型豌豆和土豆,他们生产的农产品由合作社分别以x万元/吨,y万元/吨的价格收购,他们今年种植面积、亩产量与卖出农产品的总收入如下表:
(1)求x、y的值;
(2)为了以进一步调动农户的种植热情,合作社计划明年炸收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
| 种植户 | 豌豆 | 土豆 | 卖出两种农产品总收入(万元) | ||
| 种植面积(亩) | 每亩产量(吨) | 种植面积(亩) | 每亩产量(吨) | ||
| 甲 | 4 | 1 | 4 | 3 | 4.8 |
| 乙 | 8 | 1 | 2 | 2.5 | 5.8 |
(2)为了以进一步调动农户的种植热情,合作社计划明年炸收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
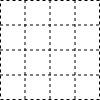 在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.
在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.