题目内容
9.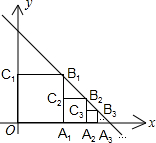 正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
分析 先根据直线的解析式,分别求得B1,B2,B3…的坐标,再根据得到的规律,求得A1,A2,A3…的坐标,最后根据得到的规律,进行求解.
解答 解:∵四边形OA1B1C1是正方形,
∴A1B1=B1C1.
∵点B1在直线y=-x+2上,
∴设B1的坐标是(x,-x+2),
∴x=-x+2,x=1.
∴B1的坐标是(1,1).
∴点A1的坐标为(1,0).
∵A1A2B2C2是正方形,
∴B2C2=A1C2,
∵点B2在直线y=-x+2上,
∴B2C2=B1C2,
∴B2C2=$\frac{1}{2}$A1B1=$\frac{1}{2}$,
∴OA2=OA1+A1A2=1+$\frac{1}{2}$,
∴点A2的坐标为(1+$\frac{1}{2}$,0).
同理,可得到点A3的坐标为(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$,0),即A3的坐标为($\frac{7}{4}$,0).
依此类推,可得到点An的坐标为(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$,0),
而1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$=$\frac{{2}^{n}-1}{{2}^{n-1}}$,
故An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
故答案是:($\frac{7}{4}$,0),($\frac{{2}^{n}-1}{{2}^{n-1}}$,0)
点评 本题主要考查了一次函数图象上点的坐标特征,需要根据一次函数的性质和坐标的变化规律进行判断分析,正确得到点的坐标变化规律是关键.解题时注意,正方形的四条边都相等,四个角都是直角.

| A. | 有两边及一角对应相等的两个三角形全等 | |
| B. | 方程x2-x+2=0有两个不相等的实数根 | |
| C. | 面积之比为1:4的两个相似三角形的周长之比是1:4 | |
| D. | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
| A. | 45 | B. | 75 | C. | 81 | D. | 135 |
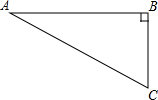 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
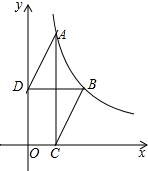 如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.
如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.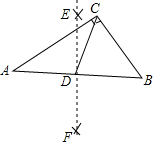 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.