题目内容
14.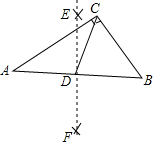 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.
分析 首先说明AD=DB,利用直角三角形斜边中线等于斜边一半,即可解决问题.
解答 解:由题意EF是线段AB的垂直平分线,
∴AD=DB,
Rt△ABC中,∵∠ACB=90°,BC=6,AC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AD=DB,∠ACB=90°,
∴CD=$\frac{1}{2}$AB=5.
故答案为5.
点评 本题考查勾股定理.直角三角形斜边中线性质、基本作图等知识,解题的关键是知道线段的垂直平分线的作法,出现中点想到直角三角形斜边中线性质,属于中考常考题型.

练习册系列答案
相关题目
6. 如图所示,a与b的大小关系是( )
如图所示,a与b的大小关系是( )
 如图所示,a与b的大小关系是( )
如图所示,a与b的大小关系是( )| A. | a<b | B. | a>b | C. | a=b | D. | b=2a |
3.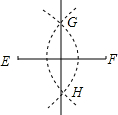 任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
 任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )| A. | △EGH为等腰三角形 | B. | △EGF为等边三角形 | ||
| C. | 四边形EGFH为菱形 | D. | △EHF为等腰三角形 |
4.n是整数,式子$\frac{1}{8}$[1-(-1)n](n2-1)计算的结果( )
| A. | 是0 | B. | 总是奇数 | ||
| C. | 总是偶数 | D. | 可能是奇数也可能是偶数 |
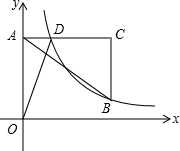 如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数$y=\frac{k}{x}(x>0)$的图象经过点B、D,且$\frac{AO}{BC}=\frac{3}{2}$.
如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数$y=\frac{k}{x}(x>0)$的图象经过点B、D,且$\frac{AO}{BC}=\frac{3}{2}$.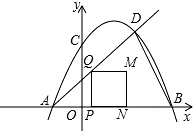 已知抛物线y=ax2+bx+c交x轴于点A(-1,0)、B(5,0),交y轴于点C(0,5),点D是该抛物线上一点,且点D的横坐标为4,连BD,点P是线段AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).
已知抛物线y=ax2+bx+c交x轴于点A(-1,0)、B(5,0),交y轴于点C(0,5),点D是该抛物线上一点,且点D的横坐标为4,连BD,点P是线段AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).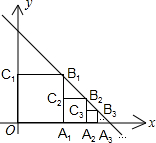 正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).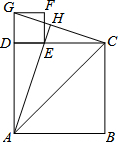 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.