题目内容
3. 如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.
如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.(1)求证:△ABE≌△CDF;
(2)若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
分析 (1)由平行四边形的性质可得AB=CD,AD=BC,且∠B=∠D,再由CE=AF,可得BE=DF,即可利用SAS定理判定△ABE≌△CDF;
(2)首先证明四边形AECF是平行四边形,再根据AE=BE,可得∠ABE=∠BAE,由∠BAC=90°可得∠ABE+∠ACE=90°,∠BAE+∠EAC=90°,再根据等角的余角相等可得∠ACE=∠EAC,进而得到AE=EC,由一组邻边相等的平行四边形是菱形证出结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,AB∥CD,
∴∠BAC=∠ACD,
∵AE平分∠BAC、CF平分∠ACD,
∴∠BAE=$\frac{1}{2}$BAC,∠FCD=$\frac{1}{2}$∠ACD,
∴∠BAE=∠DCF,
在△ABE和△CDF中$\left\{\begin{array}{l}{∠B=∠D}\\{AB=CD}\\{∠BAE=∠DCF}\end{array}\right.$,
∴△ABE≌△CDF(ASA);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵CE=AF,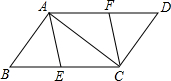
∴四边形AECF是平行四边形,
∵AE=BE,
∴∠ABE=∠BAE,
∵∠BAC=90°,
∴∠ABE+∠ACE=90°,∠BAE+∠EAC=90°.
∴∠ACE=∠EAC,
∴AE=CE,
∴平行四边形AECF是菱形.
∴四边形AECF是菱形.
点评 此题主要考查了平行四边形的性质与判定,全等三角形的判定,以及菱形的判定,关键是掌握①平行四边形的性质:平行四边形的对边相等,对角相,对角线互相平分,②菱形的判定定理:①菱形定义:一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形.

练习册系列答案
相关题目
14.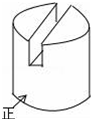 如图中几何体的左视图是( )
如图中几何体的左视图是( )
 如图中几何体的左视图是( )
如图中几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
18.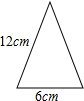 如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )
如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )
 如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )
如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | -11 |
12.下列说法正确的个数有( )
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |