题目内容
18.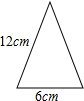 如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )
如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | -11 |
分析 根据圆锥的主视图可以得到圆锥的母线长和圆锥的底面直径,求出圆锥的底面周长就是侧面展开扇形的弧长,代入公式求得即可.
解答 解:圆锥的主视图可以得到圆锥的母线长12cm和圆锥的底面直径6cm,
∴圆锥的底面周长为:πd=6πcm,
∵圆锥的侧面展开扇形的弧长等于圆锥的底面圆的周长,
∴圆锥的侧面展开扇形的弧长为6πcm,
∴圆锥的侧面展开扇形的面积为:$\frac{1}{2}$lr=$\frac{1}{2}$×6π×12=36π,
∴$\frac{nπ×1{2}^{2}}{360}$=36π,
解得:n=90.
故选B.
点评 本题考查了圆锥的计算,解题的关键是正确地理解圆锥和侧面扇形的关系.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
9.如图,某建筑物由相同的若干个房间组成,该楼的三视图如图所示,试问:该楼有( )


| A. | 一层 | B. | 二层 | C. | 三层 | D. | 四层 |
13.等腰三角形的一个角是90°,则它的底角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.已知正六边形ABCDEF的边心距为$\sqrt{3}$cm,则正六边形的半径为( )cm.
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
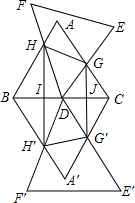 如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J. 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF. 如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.
如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.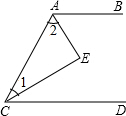 如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.
如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.