题目内容
16.如图,抛物线y=-$\frac{1}{2}$x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.(1)求抛物线的解析式;
(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
分析 (1)利用待定系数法即可解决问题.
(2)如图1中,首先证明△AOC是等腰直角三角形,由OM∥DE,推出△BMO∽△BDE,要使B、D、E为顶点的三角形与△AOC相似,只要△BOM∽△AOC,设M(0,m),可得$\frac{OM}{OB}$=$\frac{OA}{OC}$,可得$\frac{|m|}{2}$=$\frac{3}{3}$,解方程即可.
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.首先证明∠FAB=∠OMB,设M(n,0),由△AFB∽△MOB,得$\frac{OM}{AF}$=$\frac{OB}{FB}$,由此列出方程即可解决问题.
解答 解:(1)将点B(-2,0)代入抛物线的解析式y=-$\frac{1}{2}$x2+bx+3得
-$\frac{1}{2}$×(-2)2-2b+3=0,
∴b=$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3.
(2)如图1中,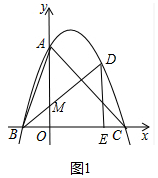
∵抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3,与x轴交于B(-2,0),A(3,0),C(0,3),
∴OA=OC,
∴△AOC是等腰直角三角形,
∵OM∥DE,
∴△BMO∽△BDE,
∵要使B、D、E为顶点的三角形与△AOC相似,
∴只要△BOM∽△AOC,设M(0,m),
∴$\frac{OM}{OB}$=$\frac{OA}{OC}$,
∴$\frac{|m|}{2}$=$\frac{3}{3}$,
∴m=±2,
∴点M的坐标为(0,2)或(0,-2).
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.
∵OA=OC,∠AOC=∠GAC=90°,
∴∠OAC=∠ACO=∠OAG=45°,
∵∠OMB+∠OAB=∠ACO=45°,
∴∠FAB=∠OMB,设M(n,0),
∵∠AFB=∠BOM=90°,
∴△AFB∽△MOB,
∴$\frac{OM}{AF}$=$\frac{OB}{FB}$,∵FB=$\frac{\sqrt{2}}{2}$,AF=$\frac{5\sqrt{2}}{2}$,OB=2,
∴$\frac{|n|}{\frac{5\sqrt{2}}{2}}$=$\frac{2}{\frac{\sqrt{2}}{2}}$,
∴n=±10,
∴点M的坐标为(0,10)或(0,-10),
∴AM=7或13.
点评 本题考查二次函数综合题、等腰直角三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键学会添加常用辅助线,构造相似三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.

 在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6-∠7的度数为( )
在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6-∠7的度数为( )| A. | 330° | B. | 315° | C. | 310° | D. | 320° |
| A. | 三角形的外角中至少有两个是钝角 | |
| B. | 直角三角形的两锐角互余 | |
| C. | 全等三角形的对应边相等 | |
| D. | 三角形三条边的垂直平分线一定交于三角形内一点 |
| A. | 1,2,4 | B. | 4,4,9 | C. | 4,5,9 | D. | 4,6,8 |
| A. | 71×102 | B. | 7.1×102 | C. | 7.1×103 | D. | 0.71×104 |
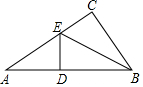 如图所示,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,则AE+DE=6cm.
如图所示,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,则AE+DE=6cm. 如图,AB为⊙O的直径,弦DA,BC的延长线相交于点P,且BC=PC,求证:∠BAD=2∠P.
如图,AB为⊙O的直径,弦DA,BC的延长线相交于点P,且BC=PC,求证:∠BAD=2∠P.