题目内容
8. 如图,AB为⊙O的直径,弦DA,BC的延长线相交于点P,且BC=PC,求证:∠BAD=2∠P.
如图,AB为⊙O的直径,弦DA,BC的延长线相交于点P,且BC=PC,求证:∠BAD=2∠P.
分析 连接AC,根据AB为圆心O的直径可知∠ACB=90°,即AC⊥BP.再根据BC=PC可知AC为BP的垂直平分线得到AB=AP,根据等腰三角形的性质得到∠P=∠B,由三角形外角的性质即可得到结论.
解答  证明:连接AC,
证明:连接AC,
∵AB为圆心O的直径,
∴∠ACB=90°,即AC⊥BP.
∵BC=PC,
∴AC为BP的垂直平分线,
∴AB=AP,
∴∠P=∠B,
∴∠BAD=∠P+∠B=2∠P.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
相关题目
13. 如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有( )
如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有( )
 如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有( )
如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
20.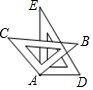 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )| A. | ∠BAD≠∠EAC | B. | ∠DAC-∠BAE=45° | C. | ∠BAE+∠DAC=180° | D. | ∠DAC>∠BAE |
17.2015年3月26日起,也门局势紧张,在亚丁湾护航的护卫舰“潍坊舰”第一时间赶到亚丁港,全力撤离中国公民,并帮助美国等承认无法帮助公民离境的国家撤侨.舰上所有官兵全力以赴,提高效率,现在撤离350人所用的时间与原计划撤离250人所用的时间相同,已知每小时实际比原计划多撤离20人,求原计划与实际撤离人员的效率.设原计划x人/小时,依题意列方程正确的是( )
| A. | $\frac{250}{x}=\frac{350}{x-20}$ | B. | $\frac{250}{x}=\frac{350}{x+20}$ | C. | $\frac{350}{x}=\frac{250}{x-20}$ | D. | $\frac{350}{x}=\frac{250}{x+20}$ |