题目内容
1.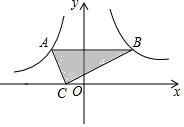 如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -1 | D. | -2 |
分析 作BD⊥x轴于点D,作AE⊥x轴于点E,由AB∥x轴知∠BCD=∠ABC=30°、∠ACE=∠BAC=60°,设点B坐标为(x,$\frac{2\sqrt{3}}{x}$),则BD=$\frac{2\sqrt{3}}{x}$、OD=x,由tan∠BCD=$\frac{BD}{CD}$求得x的值,即可知AE=BD=$\sqrt{3}$,再根据CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1得OE=2,从而得出k的值.
解答 解:如图,作BD⊥x轴于点D,作AE⊥x轴于点E,
∵AB∥x轴,
∴∠BCD=∠ABC=30°,∠ACE=∠BAC=60°,
设点B坐标为(x,$\frac{2\sqrt{3}}{x}$),
则BD=$\frac{2\sqrt{3}}{x}$,OD=x,
由tan∠BCD=$\frac{BD}{CD}$得$\frac{\sqrt{3}}{3}$=$\frac{\frac{2\sqrt{3}}{x}}{x+1}$,
解得:x=2或x=-3(舍),
∴AE=BD=$\sqrt{3}$,
在Rt△ACE中,∵CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1,
∴OE=2,
则k=-2$\sqrt{3}$,
故选:A
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
6.某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表.
根据以上信息,解答下列问题:
(1)统计表中的a=4,b0.15,c=0.3;
(2)校园小记者决定从A、B、C三位“自强自立美德少年”中,随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | c |
(1)统计表中的a=4,b0.15,c=0.3;
(2)校园小记者决定从A、B、C三位“自强自立美德少年”中,随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.

 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 如图所示,C,D是线段AB上的两点,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求线段AB的长.
如图所示,C,D是线段AB上的两点,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求线段AB的长.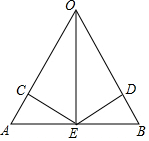 在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.
在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.