题目内容
9. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.(1)求证:AC是⊙O的切线;
(2)求图中阴影部分的面积.
分析 (1)连接OC,根据圆周角定理得到∠BOC=2∠CDB=60°,得到OC⊥BD,根据平行线的性质得到OC⊥AC,根据切线的判定定理证明结论;
(2)根据扇形的面积公式、三角形的面积公式计算即可.
解答 (1)证明:连接OC,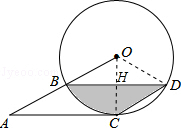
由圆周角定理得,∠BOC=2∠CDB=60°,
∵∠OBD=30°,
∴OC⊥BD,
∵AC∥BD,
∴OC⊥AC,
∴AC是⊙O的切线;
(2)解:扇形OBC的面积=$\frac{60π×{6}^{2}}{360}$=6π,
∵OB=6,∠OBH=30°,
∴OH=3,BH=3$\sqrt{3}$,
△OBH的面积=$\frac{1}{2}$×BH×OH=$\frac{1}{2}$×3$\sqrt{3}$×3=$\frac{9}{2}$$\sqrt{3}$,
△HCD的面积=$\frac{1}{2}$×6×3$\sqrt{3}$×$\frac{1}{2}$=$\frac{9\sqrt{3}}{2}$$\sqrt{3}$,
∴阴影部分的面积=6π-$\frac{9\sqrt{3}}{2}$$\sqrt{3}$+$\frac{9\sqrt{3}}{2}$$\sqrt{3}$=6π.
点评 本题考查的是切线的判定、扇形面积的计算,掌握切线的判定定理、扇形的面积公式是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
1.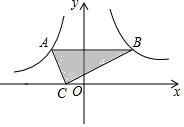 如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
 如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -1 | D. | -2 |
 已知:如图,线段a和b
已知:如图,线段a和b 在射线OM、ON分别找两点P、Q,使得四边形PQBA的周长最短.
在射线OM、ON分别找两点P、Q,使得四边形PQBA的周长最短. 如图,四点A、B、C、D,按照下列语句画出图形;
如图,四点A、B、C、D,按照下列语句画出图形;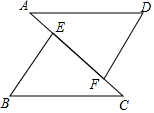 如图,AD∥BC,AD=CB,AE=CF,求证:BE∥DF.
如图,AD∥BC,AD=CB,AE=CF,求证:BE∥DF. 已知某函数的图象如图所示,求这个函数的解析式.
已知某函数的图象如图所示,求这个函数的解析式.