题目内容
17.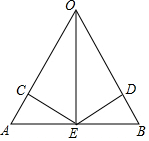 在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.
在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.
分析 利用HL定理证明Rt△ACE≌Rt△BDE,进而得到CE=DE,进而得到结论.
解答 证明:∵E是AB的中点,
∴AE=BE,
∵CE⊥BE,DE⊥BO,
∴∠ACE=∠EDB=90°,
在Rt△ACE和Rt△BDE中,
∵$\left\{\begin{array}{l}{AE=BE}\\{AC=BD}\end{array}\right.$,
∴Rt△ACE≌Rt△BDE,
∴CE=DE,
∵CE⊥AO,DE⊥BO,
∴OE是∠AOB的角平分线.
点评 本题主要考查了全等三角形的判定与性质,解题的关键是熟练掌握利用HL定理证明两个直角三角形全等,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
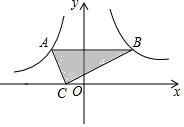 如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
 已知某函数的图象如图所示,求这个函数的解析式.
已知某函数的图象如图所示,求这个函数的解析式. 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B+∠ADE=180°.求证:BC=DE.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B+∠ADE=180°.求证:BC=DE. 如图,点O为直线AB上一点,过点O作射线OC,已知∠AOC不是直角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.
如图,点O为直线AB上一点,过点O作射线OC,已知∠AOC不是直角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE. 已知线段AB,延长线段AB至C点,使点B为AC的中点,反向延长线段AB至D点,使AD=$\frac{1}{2}$AB.
已知线段AB,延长线段AB至C点,使点B为AC的中点,反向延长线段AB至D点,使AD=$\frac{1}{2}$AB.